Simulink/Tutorials/DiffEq

This tutorial is taken from the Spring, 2010 printing of "ME125 Laboratory Exercise 1: Data Acquisition, Aliasing and Introduction to SIMULINK Modeling." It focuses specifically on the latter - an Introduction to Simulink Modeling.

Introduction

Simulink is a graphical interface type of programming environment especially useful in control systems modeling and a major tool used in both academia and industry for time dependent simulations of dynamical systems. In order to get acquainted with basic Simulink functionality, this lab will walk through how to program a simple second order harmonic oscillator with sinusoidal input

\( \begin{align} m\frac{d^2x}{dt^2}+c\frac{dx}{dt}+kx=F\sin\left(\omega t\right) \end{align} \)

where m is the mass, c represents damping, k is a restoring spring constant from Hooke’s law, F is the magnitude of the input force, and ω is the frequency of the input.

Opening Simulink

Starting window for Simulink

1. Open MATLAB and either type "simulink" in the workspace or click on the Simulink icon on the toolbar:
2. This will open the Simulink Library Browser window. The Simulink library is a categorized list of all the blocks available to write your program.
3. Next, select a new document click the icon for a new model (Simulink programs are called models and save as *.mdl). You should see an blank slate that looks like the figure at right. This is an area to drag and drop blocks and connect them together
4. We’re now ready to start building the simple harmonic oscillator model

Generating a model for the harmonic oscillator

Cascading integrators.

Generating feedback.

Adding the addder.

Model after adding Sine Wave block.

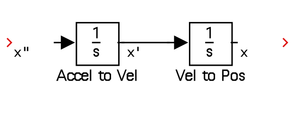
1. From differential equations and past engineering courses, you know that the harmonic oscillator model in the equation above is second order and relates the first and second derivatives of position (velocity and acceleration). We first need to construct the relationship between these two systems within the model.
2. In the Library Browser window, click on continuous on the menu and select an integrator block.
3. Drag and drop two of them into the work space and connect them between the outward pointing arrow and in the inward pointing arrow as shown in the first figure to the right in this section. The red dashed arrows were created by selecting an inward or outward pointing arrow and dragging the mouse away. The names of the blocks can be changed by double clicking on their respective titles and typing in a new name. Similarly, double clicking on a line will let you title the line.
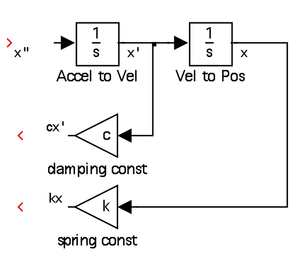
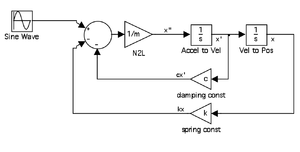
4. As you can see, SIMULINK will route the acceleration signal through two integrations to derive position. We are now in position to manipulate acceleration, velocity, and position signals as we desire by connecting other blocks to them. In the modeling equation, the damping force \(c\dot{x}\)and spring force \(kx\) can be modeled by routing the velocity and position through a gain block (found in the math operations choice in the library).
5. Drag two gain blocks into the workspace, flip them (an option found by right clicking on the block and selecting format), re-label, and connect the signals. An example of this configuration is in the second figure at right. As with nearly all SIMULINK blocks, you can change parameters by double clicking on the respective block. Since the gain is simply a multiplier, you can put any number or variable previously defined in the MATLAB workspace).
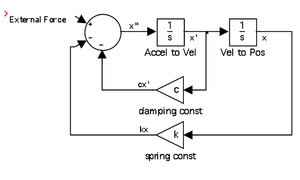
6. The next step is to add the forces together with the sum block (also in math operations). The sum block defaults to two inputs, but it can changed to as many as you want by double clicking and including another “+” or “-”. Since we will be modeling acceleration, the modeling equation can be rearranged as \(\begin{align}m\frac{d^2x}{dt^2}=F\sin\left(\omega t\right)-c\frac{dx}{dt}-kx\end{align}\)Note that the block can be enlarged after one click and resizing as if it were a jpg. You can also make the summation block rectangular by double clicking and selecting the icon shape options. The model, after attaching the feedback loops to the sum block, is the third figure at right.
7. Since the external forcing term in the differential equation is \(F\sin\left(\omega t\right)\), all we need to do is create a sinusoidal input with amplitude F. Since Simulink is designed for the type of modeling we’re doing, you can see the many input options for dynamic systems under the appropriately named sources choice on the library browser menu. Drag and drop a sine wave block and adjust the parameters by double clicking on it. Note the equation used—our amplitude is F and frequency is \(\omega\).
8. Finally, recall that acceleration is force divided by mass, so the acceleration can be isolated as:\( \begin{align} \frac{d^2x}{dt^2}=\frac{1}{m}\left(F\sin\left(\omega t\right)-c\frac{dx}{dt}-kx\right) \end{align} \)This change is reflected in the last figure at right above by the Netwon’s Second Law (N2L) gain adjustment placed between the sum block and the first integrator block.

Viewing the outputs

Model with scope.

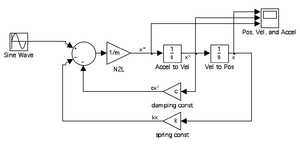
1. Within the sinks option are several options for viewing data. One very useful way is with the scope block. All you have to do is connect a display to any signal and SIMULINK will record the output in a graphical display that can be viewed by double clicking.
2. You can either connect a separate scope to any signal you want or have multiple signals route to one scope by double clicking on the block by double clicking on the scope, clicking on the parameters icon (next to the standard print icon) and changing the number of axes. If running a long time simulation, you might want to go into the data history tab and de-select the Limit data points option. Caution: sometimes too many scopes in a very large and complex simulation can slow down the simulation.
3. We’re done! Select any parameters you like for k, m, c, F, and \(\omega\) and simulate by clicking on the play button. You can adjust the simulation time by changing the value next to the stop button (the simulation time is in seconds).
4. Upon completing the simulation, click on the binoculars button in the scope to normalize all graphs so that all ranges of the data can be viewed.

Questions

Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.

References