Calculator Tips
- 3/7 Update: This page is now almost solely focused on the TI 84+ series of calculators (with a bit of a coda on TI-89). For information on the old Casio fx-991EX series, see Calculator Tips/Classwiz.
TI 84-Plus (2024 Edition)
The following guide was written while using a TI-84 Plus C Silver Edition. There are subtle differences between this edition and other (TI-84 Plus CE, for example). Anywhere "84+" shows up below refers specifically to the TI-84 Plus C Silver Edition. As exceptions are noted, they will be posted.
Using this guide
When you are given keystrokes:
- 2ND-Something means hit the 2ND key and then a key that has a secondary command of Something. For instance, 2ND-QUIT would mean hitting 2ND and then the key primarily labeled MODE, which has QUIT above it in the same color as the 2ND key
- ALPHA-Letter means hit the ALPHA key and then a key that has a letter of Letter. For instance, ALPHA-D would mean hitting ALPHA and then the key primarily labeled $$x^{-1}$$, which has D above it in the same color as the ALPHA key
- MATH-CMPLX-Command(Number) means hit the MATH button to get to the MATH menu, then use the left/right arrow buttons to scroll over to the CMPLX submenu, then use the up/down arrow buttons to scroll down to the Command command. Alternately, hit the MATH button to get to the MATH menu, then use the arrow buttons to scroll over to the CMPLX submenu, then type the Number related to the command you want. For instance, MTH-CMPLX-angle(4) will get the calculator to type
angle( - A / means use the ÷ key (÷ is annoying to type in Mediawiki)
- A * means use the $$\times$$ key (same reason)
Initial Setup
Modes
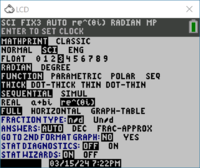
The default modes for the 84+ are not all useful for doing complex calculations. For instance, if you try to take the square root of a negative number with a factory-reset 84+, you will get an error! As a result, we recommend that you click the MODE button and then set the following modes before doing work:
- SCI (for scientific notation)
- FLOAT: 3 (to get three figures after the decimal; this yields four significant figures in scientific mode)
- RADIAN (default; for some 84+, this must be in radians to work with complex exponentials)
- re^(θi) to report using Euler notation - this will generally be the most useful as you will get a magnitude and a phase out of it
Click 2ND-QUIT to get out of this menu
Helpful Constants
There will be times that you want to quickly convert a number from degrees to radians and vice versa. Given the number of times you may need to use these conversion factors, it may be helpful to store one of them in the calculator. Here is one recommendation:
- Use letter D as the conversation from degrees to radians
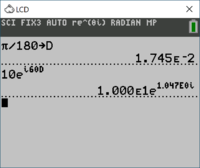
- Calculate $$\pi$$/180, then store it as D:
- 2ND-PI, ÷, 180, STO>, ALPHA-D, ENTER
- Use 1/D to convert from radians to degrees
Now if you want to calculate $$10∠60^{\circ}$$ you can type $$10e^{i60D}$$ or $$10*e^{i*60*D}$$.
If you need to get an angle in degrees from a complex number, you can use the angle() command in the MATH-CMPLX menu and then divide the result by D. For instance, to determine the angle in degrees of $$4+j5$$:
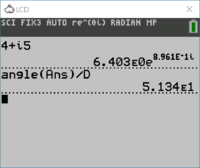
- Find $$4+j5$$ using the 84+
- 4, +, 2ND-i, 5, ENTER
- Looks like
4+i5 - reports back $$6.403E0e^{8.961E-1i}$$, so the magnitude is 6.403 and the angle is 8.961E-1=0.8961 radians
- Looks like
- 4, +, 2ND-i, 5, ENTER
- Find the angle in degrees using the
angle()command and converting the results from radians to degrees- MATH-CMPLX-angle(4), 2ND-ANS, ), ÷, D
- looks like
angle(Ans)/D - reports back 5.134E1, which is to say 51.34$$^{\circ}$$.
- looks like
- MATH-CMPLX-angle(4), 2ND-ANS, ), ÷, D
Note: a previous version of this page recommended storing 1/D in R; the problem is, there will often be times that you will be using resistor values multiple times and it makes the most sense to also store those in R, which would mean overwriting this constant. It is probably safest to just use D to go from degrees and 1/D to go from radians.
Handy Functions
Converting Representations
If you need to convert a complex number representation between rectangular and polar (and, really, Euler), make sure the value is the most recent answer and then:
- MATH-CMPLX->Rect(6) to convert an answer into rectangular (a+bi) mode
- MATH-CMPLX->Polar(7) to convert an answer into polar/Euler (re^(θi)) mode
Entering Values
Rectangular
- The 2ND and . key combination will produce $$i$$; it is represented as 2ND-i in the text
- The 84+ understands $$5i$$, $$i5$$, $$5*i$$, and $$i*5$$ to all be the same thing
- If you have an initial negative sign, you need to use the unary (-) versus the binary -
- For example, if you want just -5i, you need to enter "(-) 5 2ND-i"; starting with the regular - will generally tell the calculator to assume that you are subtracting something from the previous answer and the calculator will put Ans on the screen.
Polar
Unfortunately, the 84+ does not have an angle button for complex numbers. It does however allow for complex exponentials. Note, however, that the exponent must be in radians, regardless of the mode of the calculator! Also, some versions of the 84+ will not allow complex exponentials while in degree mode. For those that do, you have to be exceedingly careful re-using results. Best bet is to stay in (and remember that you are in) radians and convert to degrees as needed.
As an example, the polar form of $$10∠60^{o}$$ would thus be $$10e^{(π/3)}$$.
- If you are in radians model, this will work fine.
- If you are in degree mode (and after everything that has been said above, why would you be???),
- Some 84+ will give a domain error
- Others will return a value. For those that return a value,
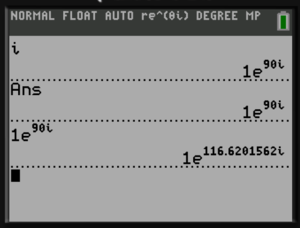
- If you are in rectangular mode, you can reuse the answer using Ans or scroll to the answer to copy and reuse it
- If you are in polar mode, you can reuse the answer using Ans but scrolling up to copy and reuse will cause a problem since the displayed angle (in degrees) will be interpreted as radians. See the figure at right for an example.
If you have an angle that is not easily converted to radians, you will need to convert degrees to radians by multiplying by $$\pi/180$$; similarly, if you find an angle in radians and want to know degrees, you will need to multiply by $$180/\pi$$. As noted above, if you have stored D as the conversion factor from degrees to radians, if you want to calculate $$10∠60^{o}$$ you can type
- 10, 2ND-$$e^x$$, 2ND-i, 60, ALPHA-D
- Displays as $$10e^{i60D}$$
- 10, *, 2ND-$$e^x$$, 2ND-i, *, 60, *, ALPHA-D
- Displays as $$10*e^{i*60*D}$$
In either case, the calculator should return $$1.000E1e^{1.047E0i}$$
Displaying Angle in Degrees
Since there are some 84+ that must be in radians to work, you may sometimes need to figure out the angle in degrees. If you have stored variable D as noted above to be $$\pi/180$$, you can use that to efficiently get the angle in degrees. Once you have performed the calculation:
- MATH-CMPLX-angle(4), 2ND-ANS, ), /, ALPHA-D, ENTER
and you will get 6.000E1 or 60 degrees.
Storing Values
If you are asked to perform complex calculations, you may want to store element values so that you can simply type a letter versus entering a number every time you use those values. For example, if a problem asks you to calculate the value of:
for a few different values of \(\omega\) (say, $$10$$ rad/s and $$10^6$$ rad/s), you could do the following on your calculator:
- Store $$1x10^{-3}$$ in L and $$5x10^{3}$$ in R:
1, 2ND-EE, (-), 3, STO>, ALPHA-L 5, 2ND-EE, 3, STO>, ALPHA-R
- Store 10 in W:
10, STO>, ALPHA-W
- Calculate $$\Bbb{H}$$ with these values:
( 2ND-i ALPHA-W ALPHA-L ) / ( 2ND-i ALPHA-W ALPHA-L + ALPHA-R )
- Once you get the result, if you want to calculate the value for a different frequency, simply typethen use the arrow buttons to go back up to where you performed the previous symbolic calculation, ENTER it to duplicate it, then ENTER it again to calculate.
1, 2ND-EE, 6, STO>, ALPHA-W
TI-89
The following information is for the TI-89 series. There are two major differences between the TI-89 and the 84+:
- The TI-89 has a < button for entering complex numbers using polar notation.
- The TI-89 will allow angles to be entered in degree mode using polar notation and will report angles in degrees using degree mode.
Setup
- To use complex numbers on a TI-89, you need to set the right mode. Hit the MODE button and set the following:
- Angle: 2: Degree
- Complex Format: 3: Polar
- The i on a TI-89 is 2ND-CATALOG
Entering Values
Euler
- The TI-89 allows for complex exponentials. Note, however, that the exponent must be in radians, regardless of the mode of the calculator! The Euler form of \(10\angle 60^o\) would thus be \(e^{(\pi/6)}\).
Polar
- The 89 has an angle button; to enter a complex number in polar notation, surround it with parentheses and separate the magnitude from the angle with the angle button, obtained with 2ND-EE. Note that the number you put in for an angle is based on the mode the calculator is in, so if you are in degree mode,
(1<60)
will be the same as
0.5+0.8660i
Displaying Values
For the TI-89:
- To show your previous answer in polar notation:
- 2nd -(ANS) 2nd 5(MATH) 4(Complex) up(to Vector Ops) right(into menu) 4(->Polar) Enter, or
- 2nd -(ANS) 2nd MODE(->) ALPHA ALPHA STO(P) -(O) 4(L) =(A) 2(R) ENTER ALPHA
- To show your previous answer in rectangular notation:
- 2nd -(ANS) 2nd 5(MATH) 4(Complex) up(to Vector Ops) right(into menu) 5(->Rect) Enter, or
- 2nd -(ANS) 2nd MODE(->) ALPHA ALPHA 2(R) /(E) )(C) T ENTER ALPHA
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.
External Links
- Complex Numbers on TI-83/84 by Stan Brown