Coordinate Systems
This page will give some pointers on converting among different representations of 2-D and 3-D vectors and surfaces as well as performing single, double, and triple integration using different coordinate systems. The basis for these systems is presented, followed by several examples of these systems at work and transformations between them.
Contents
Conversion Charts
First, it is important to know how to convert among the different coordinate systems. The following sections give the 2-D and 3-D conversions; in each table, the conversions are functions for the variable given on the left in terms of the variables of the system specified in the top row.
2-D Conversions
To get a mental picture of 2-D conversions, imagine a line from the origin to the point \((x,y)\). The length of this line is the radius \(r\), and the angle it makes with the positive \(x\) axis is the angle \(\theta\). The Cartesian coordinates therefore give you the \(x\) and \(y\) components while the polar coordinates give you the total length and the direction.
3-D Conversions
To get a mental picture of 3-D conversions, imagine a line from the origin to the point \((x,y,z)\). The length of this line is the spherical radius \(\rho\). The shadow of \(\rho\) on the \(xy\) plane looking from above is the cylindrical radius \(r\). The angle between the shadow and the positive \(x\) axis is \(\theta\), and the minimum angle between the actual line and the positive \(z\) direction is the angle \(\phi\). For the coordinate direction scheme, the angles \(\alpha\), \(\beta\), and \(\gamma\) represent the minimum angle between the line and the \(x\), \(y\), and \(z\) axes, respectively.
Unit Areas and Volumes for Integration
When using different coordinate systems for integrating, you must use conversions are for incremental areas and volumes. They are:
These area and volume conversions are extremely important. Forgetting the extra \(r\) or \(\rho^2~\sin\phi\) will clearly get the wrong answer and will occasionally make an integral much harder than was intended.
Tips
Different coordinate systems have different advantages. One way to see this is to imagine what shapes you can make by holding one of the variables fixed and letting the others take all possible values.
In two dimensions, keeping \(x\) or \(y\) constant gives either a vertical or horizontal line. Simple functions of \(x\) and \(y\) give lines at any angle and any intercepts. Keeping \(r\) constant gives a circle. Keeping \(\theta\) constant yields a straight line through the origin. Simple functions of \(r\) and \(\theta\) can give shifted circles, lemniscates, spirals, or many other interesting shapes.
In three dimensions, keeping \(x\), \(y\), or \(z\) constant gives a plane. Simple (no squares) functions give planes at any angle and intercept. For cylindrical coordinates, keeping \(z\) or \(\theta\) constant gives a plane - either parallel to the \(xy\) plane or at some angle through the \(x\) axis perpendicular to the \(xy\) plane - while a constant \(r\) gives a cylinder. This is especially useful for problems whose geometries are symmetric about the \(z\) axis.
Spherical coordinates have the richest variety. Keeping \(\rho\) constant yields a sphere, \(\theta\) constant yields a plane, and \(\phi\) constant yields a cone. Any problem having some combination of these geometries is well-suited to spherical coordinates.
Deciding when to use what coordinate system takes practice. In general, if you have spherical symmetry in the boundaries or an \(x^2+y^2+z^2\) term in the function you will use spherical. If you have cylindrical symmetry or an \(x^2+y^2\) term, you will generally use cylindrical coordinates. It is often difficult to determine which integral is on the inside and which is on the outside, especially when doing triple integrals.
Examples
1: Moment of Inertia
Find the moment of inertia about the \(z\)-axis of a solid, constant-density cylinder \(x^2+y^2\leq R^2\), \(0\leq z\leq H\).
To find this answer, first figure out what coordinate system to solve this in. Since it is a cylinder, cylindrical coordinates seem the easy answer. Given the shape, the independent variable can be either \(r\) or \(\theta\). The \(z\) integral has to be on the inside. One possible solution is below; note that \(\rho_{\mbox{density}}\) is used to denote density and differentiate it from the \(\rho\) of the spherical coordinate system.
This matches tables for such a shape, which state that a cylinder has a rotational moment of inertia
2: Volume
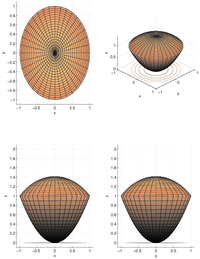
Find the volume of the region bounded above by the spherical surface \(x^2+y^2+z^2=2\) and below by the paraboloid \(z=x^2+y^2\).
Again, the volume of intersection is cylindrical. It is simple in \(z\), so that will be the innermost integral. \(r\) will be chosen for the outer integral, so we need to get the intersection:
so the limits on \(r\) are \(0\) and \(1\):
Caution!
It is important to note here that the use of the particular symbols on this page is not universally accepted. Here, \(\theta\) is used as the azimuthal angle and \(\phi\) is the inclination angle. The international standard ISO 80000-2:2009, changes the symbols for the angles around. For this reason, it is important to note that various sources may use different notations. Wikipedia, for instance, generally follows ISO 80000-2:2009 but not always since many of the editors are used to the notation as given in this document. The article Spherical Coordinates[1] discusses the issue and also provides a diagram of the different coordinate systems. Note that the article uses \(r\) for the spherical radius instead of \(\rho\) - which seems a bit odd since their article Cylindrical Coordinates[2] uses \(r\) also as the radial coordinate.
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.
External Links
References
- ↑ Weisstein, Eric W. "Spherical Coordinates." From MathWorld--A Wolfram Web Resource. Accessed 5/18/2010
- ↑ Weisstein, Eric W. "Cylindrical Coordinates." From MathWorld--A Wolfram Web Resource. Accessed 5/18/2010