Calculator Tips

From PrattWiki
Revision as of 20:55, 7 March 2024 by DukeEgr93 (talk | contribs)
Jump to navigation Jump to search
  • 2/24/2024 update - the Casio fx-991EX has recently been discontinued in favor of the fx-991CW. More soon on whether that will become the new recommended calculator or not.
  • 2/26/2024 update - the vast majority of respondents to a calculator survey for ECE 110 and EGR 224 indicate having a TI-84 Plus of some kind, so this page will be reorganized accordingly.

This page contains information about how to use various calculators for different classes.

TI 84-Plus (2024 Edition)

The following guide was written while using a TI-84 Plus C Silver Edition. There are subtle differences between this edition and other (TI-84 Plus CE, for example). Anywhere "84+" shows up below refers specifically to the TI-84 Plus C Silver Edition. As exceptions are noted, they will be posted. When you are given keystrokes:

  • 2ND-Something means hit the 2ND key and then a key that has a secondary command of Something. For instance, 2ND-QUIT would mean hitting 2ND and then the key primarily labeled MODE (that has QUIT above it in the same color as the 2ND key)
  • ALPHA-Letter means hit the ALPHA key and then a key that has a letter command of Letter. For instance, ALPHA-D would mean hitting ALPHA and then the key primarily labeled $$x^{-1}$$ (that has D above it in the same color as the ALPHA key)
  • MATH-CMPLX-Command(Number) means hit the MATH button to get to the MATH menu, then use the arrow buttons to scroll over to the CMPLX submenu, then use the arrow buttons to scroll down to the Command command. Alternately, hit the MATH button to get to the MATH menu, then use the arrow buttons to scroll over to the CMPLX submenu, then type the Number related to the command you want. For instance, MTH-CMPLX-angle(4) will get the calculator to type angle(

Initial Setup

Modes

The default modes for the 84+ are not all useful for doing complex calculations. For instance, if you try to take the square root of a negative number with a factory-reset 84+, you will get an error! As a result, we recommend that you click the MODE button and then set the following modes before doing work:

  • SCI (for scientific notation)
  • FLOAT: 3 (to get three figures after the decimal; this yields four significant figures in scientific mode)
  • RADIAN (default; for some 84+, this must be in radians to work with complex exponentials)
  • re^(θi) to report using Euler notation - this will generally be the most useful as you will get a magnitude and a phase out of it

Click 2ND-QUIT to get out of this menu

Helpful Constants

There will be times that you want to quickly convert a number from degrees to radians and vice versa. Given the number of times you may need to use these conversion factors, it may be helpful to store them in the calculator. Here is one recommendation:

  • Use letter D as the conversation from degrees to radians and use letter R as the conversion from radians to degrees
  • Calculate $$\pi$$/180, then store it as D:
    • 2ND-PI, ÷, 180, ENTER
    • STO>, ALPHA-D, ENTER
  • Use 1/D to store R:
    • 1, ÷, ALPHA-D, ENTER
    • STO>, ALPHA-R, ENTER

Now if you want to calculate $$10∠60^{\circ}$$ you can type $$10e^{i60D}$$ or $$10*e^{i*60*D}$$. If you need to get an angle in degrees from a complex number, you can use the angle() command in the MATH-CMPLX menu and then multiply the result by R. For instance, to determine the angle in degrees of $$4+j5$$:

  • 4, +, 2ND-i, 5, ENTER
    • reports back $$6.403E0e^{8.961E-1i}$$, so the magnitude is 6.403 and the angle is 8.961E-1=0.8961 radians
  • MATH-CMPLX-angle(4), 2ND-ANS, ), *, R
    • reports back 5.134E1, whish is to say 51.34$$^{\circ}$$.

Handy Functions

Converting Representations

If you need to convert a complex number representation between rectangular and polar:

  • Hit MATH, then arrow over to the CMPLX menu
  • Hit 6 if you want to go into rectangular and 7 if you want to go into polar
  • Hit ENTER

Entering Values

Rectangular

  • The "2ND ." key combination will produce $$i$$.
  • The 84+ understands $$5i$$, $$i5$$, $$5*i$$, and $$i*5$$ to all be the same thing
  • If you have an initial negative sign, you need to use the unary (-) versus the binary -
    • For example, if you want just -5i, you need to enter "(-) 5 i"; starting with the regular - will generally tell the calculator to assume that you are subtracting something from the previous answer (Ans).

Polar

TI-84 Plus C SE showing potential issue using radian-based exponentials in degree mode

Unfortunately, the 84+ does not have an angle button for complex numbers. It does however allow for complex exponentials. Note, however, that the exponent must be in radians, regardless of the mode of the calculator! Also, some versions of the 84+ will not allow complex exponentials while in degree mode. For those that do, you have to be exceedingly careful re-using results.

As an example, the polar form of $$10∠60^{o}$$ would thus be $$10e^{(π/6)}$$.

  • If you are in radians model, this will work fine.
  • If you are in degree mode,
    • Some 84+ will give a domain error
    • Others will return a value. For those that return a value,
      • If you are in rectangular mode, you can reuse the answer using Ans or scroll to the answer to copy and reuse it
      • If you are in polar mode mode, you can reuse the answer using Ans but scrolling up to copy and reuse will cause a problem since the displayed angle (in degrees) will be interpreted as radians. See the figure at right for an example.

If you have an angle that is not easily converted to radians, you will need to convert degrees to radians by multiplying by $$\pi/180$$; similarly, if you find an angle in radians and want to know degrees, you will need to multiply by $$180/\pi$$. Given the number of times you may need to use these conversion factors, it may be helpful to store them in the calculator. Here is one recommendation:

  • Use letter D as the conversation from degrees to radians and use letter R as the conversion from radians to degrees
  • Calculate $$\pi$$/180, then type ANS STO> ALPHA D ENTER
  • Calculate 1/D, then type ANS STO> ALPHA R ENTER

Now if you want to calculate $$10∠60^{o}$$ you can type $$10e^{i60D}$$ or $$10*e^{i*60*D}$$

Displaying Angle in Degrees

Since there are some 84+ that must be in radians to work, you may sometimes need to figure out the angle in degrees. If you have stored variable R as noted above to be $$180/\pi$$, you can use that to efficiently get the angle in degrees. Once you have performed the calculation:

  • Click MATH, scroll to CMPLX, 4 (for angle()
  • Click Ans
  • Click ) * ALPHA R

CLASSWIZ

Complex mode

For the CLASSWIZ to work with complex values, it needs to be in complex mode:

  • Turn the calculator on
  • Hit the Menu button
  • Hit 2 for complex

To test this, try calculating the square root of negative 1. If you get a math error, you are in the wrong mode.

Other settings

  • For input and output representations - you will most likely want to set the calculator to Math Input and Decimal Output. See p. 5 of the user's guide.
    • Hit Shift and then Menu/Setup
    • Hit 1 for Input/Output
    • Hit 2 for MathI / Decimal0
This will automatically convert items to floating point rather than leaving raw square roots, $$\pi$$, and the like. If you want to convert back and forth quickly, use the $$S\leftrightarrow D$$ button.
  • For angles:
    • Hit shift and then Menu/Setup
    • Hit 2 for Angle Unit
    • Pick the unit you will generally be using - most likely degrees- all input and output will use these units for angles.
      • If you want to specify a different input unit during a calculation, enter the number then Option-Up-2 and choose the unit. If your calculator is in radian mode, for instance $$1\angle 45$$ will give you the result for 1 at 45 radians while $$a\angle 45^o$$ will give you the results for 45 degrees(even in radians mode).
  • To display values in a particular way:
    • Hit Shift and then Menu/Setup
    • Hit 3 for Number Format
    • Sci (2) and then 5 tends to be a pretty useful way to go.
  • To set the complex number display to the way you like it:
    • Hit Shift and then Menu/Setup
    • Scroll down one page and then type 2 for Complex
    • Choose either rectangular or polar coordinates


Entering Values

Cartesian

Enter the real part, followed by the sign of the imaginary part, followed by $$i$$ or $$x~i$$. Note that if the real part is negative, or if the real part is 0 and the imaginary part is negative, you need to use the unary (-) versus the binary -.

Polar

Enter the magnitude, followed by the angle symbol (SHIFT ENG), followed by the angle in the appropriate units for how your calculator is set. Note that the magnitude must be non-negative! If you have a negative magnitude for a number by itself (for instance, $$-2\angle 30^o$$, you either need to enter it as 0- that number ($$0-2\angle 30^o$$) or you need to change the angle by $$\pm180^o$$ ($$2\angle -150$$)

Displaying Values

  • To show your previous answer in polar notation:
    • OPTN
    • Down
    • 1
    • =
  • To show your previous answer in rectangular notation:
    • OPTN
    • Down
    • 2
    • =

Complications

  • The CLASSWIZ will not accept complex numbers in polar form with negative magnitudes. You can subtract a number from another, but you can not have the unary negative in front of a magnitude.
  • The CLASSWIZ will not do roots of complex numbers.


TI 83+, 84+, 89

  • To use complex numbers on a TI-89, you need to set the right mode. Hit the MODE button and set the following:
    • Angle: 2: Degree
    • Complex Format: 3: Polar
  • The 83, 84, and 89 all have the \(i\). For 83/84 it is "<2ND> ." (that is, the 2nd function button at top left followed by the decimal point in the bottom row) and for the 89 it is "<2ND> <CATALOG>"; entering a complex number in Cartesian form is thus as simple as multiplying the imaginary part by \(i\).

Euler

  • The 83, 84, and 89 all allow for complex exponentials. Note, however, that the exponent must be in radians, regardless of the mode of the calculator! The Euler form of \(10\angle 60^o\) would thus be \(e^{(\pi/6)}\).
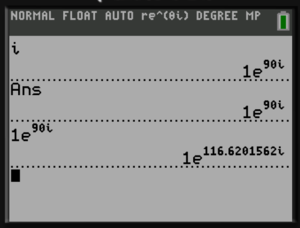
    • For the 83, if you are in degree mode, the results will be in degree mode but the inputs must always be in radians. For instance,
e^(i*90)

returns 

1e^(116.62i)

if the calculator is in degree mode since 90 radians simplifies to 116.62 degrees. It returns 

1e^(2.035i)

if the calculator is in radian mode since 90 radians is the same as 90-28\(\pi\) is 2.035 radians.

    • For the 84, the results are the same as for the 83 however you must be very careful if you try to use the result from a complex calculation that is reported in degree mode. On an 84, if you enter
e^(i*90)

the result, in degree mode, is 

1e^(116.62i)

If you try to up-arrow to that result and hit <ENTER> to copy it, then use it, the 84 will think of the 116.62 as a value in radians - which is to say, not at all what you meant! If you are in degree mode, you need to refrain from using the Euler representation on an 84 or at least understand that intermediate results in Euler mode and degree mode together cannot be used later.

    • For the 84, the calculator will not let you use Euler representation if you are in degree mode - you will get a domain error. To use Euler representations on an 84, you will have to be in radian mode.

Polar

  • Neither the 83 nor the 84 use polar representation. You have to use Euler if you have a magnitude and an angle, and the angle must be entered in radians.
  • The 89 has an angle button; to enter a complex number in polar notation, surround it with parentheses and separate the magnitude from the angle with the angle button, obtained with <2ND> <EE>. Note that the number you put in for an angle is based on the mode the calculator is in, so if you are in degree mode,
(1<60)

will be the same as 

0.5+0.8660i

Displaying Values

For the TI-89:

  • To show your previous answer in polar notation:
    • 2nd -(ANS) 2nd 5(MATH) 4(Complex) up(to Vector Ops) right(into menu) 4(->Polar) Enter, or
    • 2nd -(ANS) 2nd MODE(->) ALPHA ALPHA STO(P) -(O) 4(L) =(A) 2(R) ENTER ALPHA
  • To show your previous answer in rectangular notation:
    • 2nd -(ANS) 2nd 5(MATH) 4(Complex) up(to Vector Ops) right(into menu) 5(->Rect) Enter, or
    • 2nd -(ANS) 2nd MODE(->) ALPHA ALPHA 2(R) /(E) )(C) T ENTER ALPHA

Storing Values

If you are asked to perform complex calculations, you may want to store element values so that you can simply type a letter versus entering a number every time you use those values. For example, if a problem asks you to calculate the value of:

\( \begin{align} \Bbb{H}(j\omega)=\frac{j\omega L}{j\omega L + R}\\ L=1\mbox{mH}, R=5\mbox{k}\Omega \end{align} \)

for a few different values of \(\omega\) (say, $$10$$ rad/s and $$10^6$$ rad/s), you could do the following on your calculator:

CLASSWIZ

The CLASSWIZ only has the letters A, B, C, D, E, F, x, y, and M to store, so you have to choose where to store things. For this example, we will store the inductor value in A and the resistor value in B. Also note that once you hit the STO key, you will not need to hit the ALPHA button to indicate the letter. In the keystrokes below then, the A really means hitting the (-) key and the B means hitting the...one next to it... 

1 <x10x> (-) 3 <STO> A
5 <x10x> 3 <STO> B

We will store the frequency component in x: 

10 * i <STO> x

to store the values. Then, to calculate the first value, 

( <ALPHA> x * <ALPHA> A ) / ( <ALPHA> x * <ALPHA> A + <ALPHA> B )

and you should get $$2.0000x10^{-6}\angle 9.0000x10^1$$ Once you get the result, if you want to calculate the value for a different frequency (say, $$10^6$$), simply type 

1 <x10x> 6 * <2ND> i <STO> x

then use the arrow buttons to go back up to where you performed the previous symbolic calculation, and hit the = key to recalculate. You will now get $$1.9612x10^{-1}\angle 8.8690x10^1$$.


TI

1e-3 <STO>> <ALPHA> l
5e3 <STO>> <ALPHA> r

To store the frequency component, on TI 83/84 plus, you will need to use ALPHA z, while on the TI 89 you can just use the z button: 

10 * 2ND i STO> (ALPHA) z

to store the values. Then, to calculate the first value, 

( <ALPHA> z * <ALPHA> l ) / ( <ALPHA> z * <ALPHA> l + <ALPHA> r )

Once you get the result, if you want to calculate the value for a different frequency, simply type 

1e6 * <2ND> i <STO>> <ALPHA> z

then use the arrow buttons to go back up to where you performed the previous symbolic calculation, ENTER it to duplicate it, then ENTER it again to calculate.

Constant of Angle Conversion

If you are doing several complex calculations on an 83/84 and the angles you are given are in degrees, you may want to store a constant for the conversion to radians so you do not have to type in "* pi / 180" every time. You could just put in 

pi / 180 <STO>> D

and then when you need to write a complex number in Euler form, you could multiply the angle in degrees by D; for instance, to get 6<30 degrees, you could write 

6*e^(i*30*D)

You can choose any letter, obviously.

Statics Functions

TI-83/84

Not as many built-in functions for vectors / matrices. See http://www.tc3.edu/instruct/sbrown/ti83/vecprod.htm for a program that will help with cross products.

TI-89

Vectors in General

Vectors may be entered surrounded by [ ]. That is, for some vector \(\vec{r}\):

\( \begin{align} \vec{r}&=r_x\hat{\imath}+r_y\hat{\jmath}+r_z\hat{k} \end{align} \)

say,

\( \begin{align} \vec{r}&=3\hat{\imath}-2\hat{\jmath}+6\hat{k} \end{align} \)

the TI version of the vector would be: 

[3, -2, 6]

Note that the result will actually be surrounded by two sets of square brackets, representing a matrix. Be sure to use the unary negative operator (-) versus the binary subtraction operator - at the start of negative entries.

Dot and Cross Products

Unit Directions

  • To find the unit direction for a vector, use
    • <2nd>--<5>MATH--<4>Matrix--L:Vector ops--<1>unitV()

Coordinate Angles

  • To find the coordinate angles of a vector, you should first get the unit direction vector. Then, you must turn the unit direction vector into a list before taking the arccos of the list. Lists are surrounded by {} instead of []. To convert a vector to a list, use
    • <2nd>--<5>MATH--<3>List--F:mat->list()
      and put the desired matrix in as the argument; the result will be surrounded by {}. You can then apply the arccos to the list and get all three coordinate direction angles at once!

Questions

Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.

External Links

References

Retrieved from "https://pundit.pratt.duke.edu/piki/index.php?title=Calculator_Tips&oldid=30863"