Python/Phasors
This page contains handy Python functions and processes for use with Phasors and Phasor analysis.
Contents
Modules
Everything below assumes:
import numpy as np import sympy as sym
Processes
Entering a numerical value for phasor or complex number
Python will allow you to enter a complex number as NR + NIj; for example, 3 + 2j. Note that there needs to be a number before the j; if you try a=3 + j you will get an error whereas a = 3 + 1j will work.
For polar representations, you can use the function below:
def polar(mag, ang, units='deg'):
if units=="deg":
ang = ang * np.pi / 180
return mag * np.exp(1j * ang)The default is degrees - if the third argument is anything other than 'deg' the result will be calculated based on radians.
Obtaining magnitude and phase values
To get the magnitude of a complex number, use the abs command. To get the angle, use np.angle(x) but keep in mind the angle will be in radians. To get the angle in degrees, use np.angle(x, True)
Calculating Parallel Impedances
The following process par will calculate a numerical or symbolic value for some set of parallel impedances:
def par(*args):
inv = 0
for k in args:
inv += 1/k
return sym.simplify(1/inv)Simplifying solutions
You may need to use the complex(THING) command to reduce complicated forms of complex numbers to a single complex number.
Reporting Single Complex Number in Polar Form
The following process will display the magnitude and phase angle (in degrees by default):
def printphasor(N, units='deg'):
N = complex(N)
ang = np.angle(N)
un = 'rad'
if units=='deg':
ang = ang * 180 / np.pi
un = 'deg'
print("{:g} < {:+0.3f} {}".format(abs(N), ang, un))Reporting Phasors Solution List as Magnitudes and Angles in Degrees
Maple can be asked to process a list of results to report them as phasors. The listphasors command takes an input argument that comes from the solve command and prints the results as a table of variables, magnitudes, and angles in degrees. The command is given below in the next section.
Handy commands
Given the above, here is a list of the handy commands that can be copied into the beginnings of a Python worksheet:
import numpy as np
import sympy as sym
sym.init_printing(order="grevlex") # orders polynomials from highest to lowest
def polar(mag, ang, units='deg'):
if units=="deg":
ang = ang * np.pi / 180
return mag * np.exp(1j * ang)
def par(*args):
inv = 0
for k in args:
inv += 1/k
return sym.simplify(1/inv)
def listphasors(sols, units='deg'):
for key in sols.keys():
cval = complex(sols[key])
mag = abs(cval)
ang = np.angle(cval)
un = 'rad'
if units=='deg':
ang = ang * 180 / np.pi
un = 'deg'
print("{} = {:0.5g} < {:+0.3f} deg".format(key, mag, ang))
(whee!)
Examples
The following are PDFs of the Maple worksheet used to solve the problems listed.
- Alexander & Sadiku Practice Problem 10.1 (single frequency) PDF
- Alexander & Sadiku Example Problem 10.6 (three frequencies) PDF
- The worksheet uses following labels (adapted from Fundamentals of Electric Circuits, Charles Alexander & Matthew Sadiku, 5th ed., McGraw-Hill, 2013)
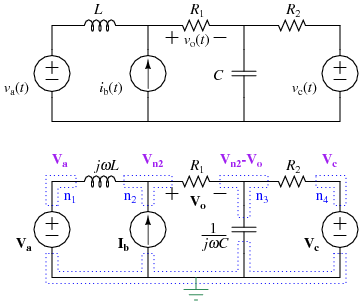
- Svoboda & Dorf Example 10.8-1 (two frequencies) PDF