MATLAB:Fminbnd and fminsearch

The fminbnd command in MATLAB can be used to find the value of a single parameter of a multivariable function that will minimize the value of the function on some bounded domain. The command can only find one minimum at a time and can only find minima based on one variable at a time. If there is a single local minimum over the domain, fminbnd should find it. If there are several, it should find one of them, though it may not find the most minimum minima. If there is no local minimum in the range, fminbnd will return one of the boundary values, depending on where the function is at its minimum value for the domain. There are several different ways to present fminbnd with the specific function and variable.

Examples

Different Function Calls

Most General Case

The following examples show a method that will work regardless of how many input variables your function has or how you define your function - whether it is built-in, a variable containing an anonymous function, an anonymous function generated on the fly, or a .m file function. The paradigm is:

[INDEP_AT_MIN, FUNCTION_MIN] = fminbnd(@(DUMMY_VAR) FUNCTION_THING, LEFT_INDEP, RIGHT_INDEP)

where

• INDEP_AT_MIN is the calculated value of the requested variable when the function is at a minimum in the domain
• FUNCTION_MIN is the minimum value of the function at the INDEP_AT_MIN location
• DUMMY_VAR is the variable you want to use in this FUNCTION_THING to indicate which of the various inputs fminbnd is allowed to alter
• FUNCTION_THING can be a built-in function, the name of an anonymous function, the name of a .m file function, or a calculation - whatever it is that you are trying to minimize; note that DUMMY_VAR must appear somewhere in this expression for fminbnd to be able to do anything
• LEFT_INDEP, RIGHT_INDEP represent the minimum and maximum value of the range over which you want to minimize the function.

Plot showing the function on the domain between -10 and 10

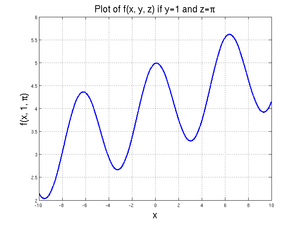
The example is based on wanting to determine minimum (and later, maximum) values of:

\(f(x, y, z)=\frac{x}{10}+\cos(x)+\sin(y)+z\,\!\)

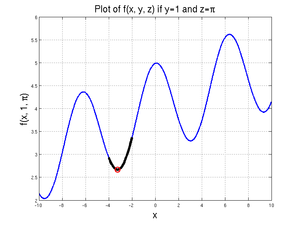
We will assume that two of the three variables (\(y\) and \(z\)) are known and that we want to find \(x\) given those values. We will further assume that \(y=1\) and \(z=\pi\). A graph of this function for values of \(x\) between -10 and 10 is shown at right.

Function on the Fly

If you only want to solve this problem once, and the calculation only requires one line of code, the process with the least "overhead" involves creating the function on the fly inside the fzero command. All you have to do is put your expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. You will also need to specify the boundary values.

Plot focusing on domain between 0 and 5 showing minimum at 3.0414

The line:

[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, 0, 5)

will produce

xValue =
   3.0414e+00
fValue =
   3.2922e+00

which has found the local minimum between \(x=0\) and \(x=5\).

Plot focusing on domain between 5 and 7 showing minimum at 5.0000

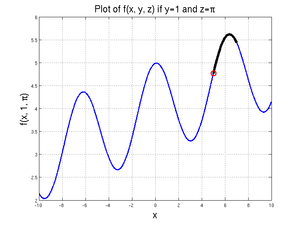
Running the code:

[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, 5, 7)

will produce

xValue =
   5.0000e+00
fValue =
   4.7668e+00

since, for \(x\) values between 5 and 7, there is no local minimum. The value of the function at 5 is less than the value of the function at 7, so the 5 is returned.

Plot focusing on domain between -9 and 10 showing "minimum" at 3.0414

Plot focusing on domain between -4 and -2 showing minimum at -3.2418

Finally, for

[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, -9, 10)

MATLAB returns:

xValue =
   3.0414e+00
fValue =
   3.2922e+00

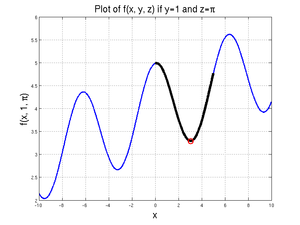
Note that this is not actually the "minimum" minimum - that would be at \(x=-3.2418\), where the function is 2.6639, as given by

[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, -4, -2)

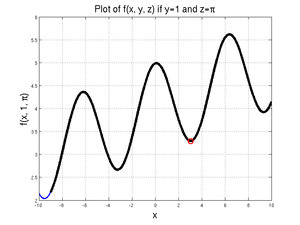
Furthermore, the actual minimum value of the function over the domain from -9 to 10 is given at \(x=-9\), where \(f=2.1719\); since MATLAB was able to find at least one local minimum, however, it did not check the boundary values.

A slightly "longer" version of this would have you pre-define the \(y\) and \(z\) variables first, then use the variables in the function definition: expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. The line:

y = 1;
z = pi;
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(y) + z, -4, -2)

This works the same as the last example above - recall that when anonymous functions are created, they can take "snapshots" of the workspace. In the case above, the FUNCTION_THING is able to "see" what the variables y and z contain.

Pre-Defined Functions

If you want to solve the same problem multiple times, perhaps by altering initial guesses or altering one or more of the constant parameters in the function, you should first define the function. If the expression can be calculated all on one line, you may choose to use a variable with an anonymous function - for example:

MyFun = @(xa, ya, za) xa/10 + cos(xa) + sin(ya) + za

On the other hand, if the expression is more complicated or if you just want to put it in a .m file, you can certainly do that as well. or example, instead of the MyFun variable above, you could write a MyFun.m file containing:

function out = MyFun(xb, yb, zb)
out = xb/10 + cos(xb) + sin(yb) + zb;

In either case, you would use fminbnd by properly building the FUNCTION_THING using the name of the function. As in the previous example, you can hard-code the values for the \(x\) and \(y\) values:

[xValue, fValue] = fminbnd(@(xDummy) MyFun(xDummy, 1, pi), -4, 2)

or you can use variables to transmit the information:

y = 1;
z = pi;
[xValue, fValue] = fminbnd(@(xDummy) MyFun(xDummy, y, z), -4, 2)

In any event, note again that the FUNCTION_THING only has one unknown, and that unknown is named as the DUMMY_VAR.

==== Single-Variable Anonymous Functions ====

For single-variable anonymous functions, there is a slightly simpler way to run fminbnd - all you need to do is give the name of the variable to FUNCTION_THING rather than setting up the DUMMY_VAR. For example, to find the minimum value of \(x^2-\cos(x)=0\) on the domain from \(x\) going from -2 to 3, you can set up an anonymous function for it as:

MyAnonCalc = @(x) x.^2-cos(x)

and then solve with:

[xValue, fValue] = fminbnd(MyAnonCalc, -2, 3)

to get

xValue =
  -4.5124e-07
fValue =
  -1.0000e+00

Single-Variable Built-in Functions and .m Functions

The following method works for both built-in single-input functions and .m file single-input functions (i.e. not variables containing anonymous functions). The first argument is the name of the function in single quotes and the second argument is the initial guess or initial bracket for the one variable of the function. For example, to find the minimum value of \(\cos(x)\) for the domain of \(x\) going from 0 to 4, you can type

[xValue, fValue] = fminbnd('cos', 0, 4)

and get

xValue =
   3.1416e+00
fValue =
  -1.0000e+00

If you have a .m file function of one variable, the process is the same. For example, to find the minimum value of \(y=x^2-\cos(x)\) on a domain from -2 to 3, you could first create a .m file called MyCalc.m with:

function out = MyCalc(in)
out = in.^2 - cos(in);

then use fminbnd:

[xValue, fValue] = fminbnd('MyCalc', -2, 3)

and get

xValue =
  -4.5124e-07
fValue =
  -1.0000e+00

Finding Maximum Values

Plot focusing on domain between 5 and 7 showing maximum at 6.3834

There is no fmaxbnd command. Conveniently, all you need to do to figure out the value and location of the maximum values would be to give fminbnd your function multiplied by -1. The only problem here is that the value of the function fminbnd returns will be the opposite of what you want. For example:

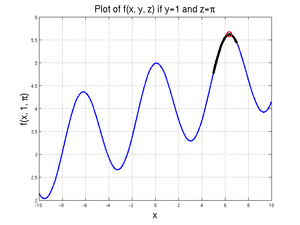
[xValue, fValueSignWrong] = fminbnd(@(xDummy) -(xDummy/10 + cos(xDummy) + sin(1) + pi), 5, 7)

will return

xValue =
   6.3834e+00
fValueSignWrong =
  -5.6164e+00

in order to get the actual value of the function at a maximum, you would need to re-run the calculation or just create a new variable that is equal to -1 multiplied by the function value MATLAB gave:

[xValue, fValueSignWrong] = fminbnd(@(xDummy) -(xDummy/10 + cos(xDummy) + sin(1) + pi), 5, 7)
fValue = -1*fValueSignWrong

to get

xValue =
   6.3834e+00
fValueSignWrong =
  -5.6164e+00
fValue =
   5.6164e+00

Questions

Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.

References