Maple/Differential Equations/RC Example
Contents
Description
The following page will go through an example of using Maple's ability to work with differential equations to analyze a circuit that undergoes a change in source values. In this particular case, the independent source is given as a constant for all times before 0 sec, at which time it changes to a non-constant source. The source is connected to a network containing both resistors and a capacitor. While there are several ways to put all this work together in a Maple script, the following will provide a flexible framework for solving the equations and using substitution to determine a numerical list of initial conditions, substituting element values into the differential equations and putting them into a list, solving the differential equations, and finally plotting the results.
Circuit
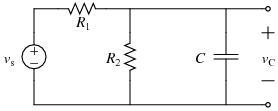
For this demonstration code, the following circuit is used:
where \(R_1\)=20 k\(\Omega\), \(R_2\)=30 k\(\Omega\), \(C\)=50 \(\mu\)F, and \(v_s(t)\) changes from 5 V to 10 cos(8\(t\)) V when \(t=0\) s.
DC Steady-State Analysis
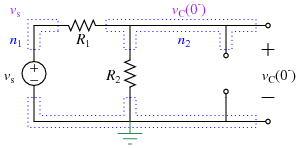
Assuming the circuit has been in place for a "long time" before \(t\)=0 sec, and given the topology of the circuit and the fact that the independent source is a constant for all times before 0 sec, you can use the DC steady-state equivalent for the circuit at \(t=0^-\) sec:
Using KCL at the top right node gives:
which can be solved to find the capacitor voltage at the time just before the source \(v_S(t)\) changes.
Model Equations for t>0
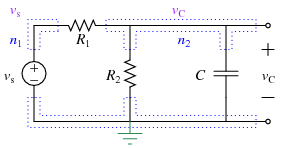
In general, after \(t\)=0 sec you can label the circuit as:
Using KCL at the top right node again gives:
Code
Now that the equations for DC steady state and for the differential model are known, you can write Maple code to solve for everything.
Preparing the Worksheet
Be sure that your name and the assignment show up as text at the top
of the page. Also be sure that the first Maple command is restart.
Values
Create a list of values for substitutions later. Note that there should probably be one variable for the DCSS steady-state analysis and another for the differential equations. In this case, vsDC will be the $$t<0$$ value and vs(t) will be for $$t\geq 0$$.
Initial Conditions From Steady-State
While Maple can solve differential equations with symbolic initial conditions and coefficients, most of the time this will result in a very unwieldy and unhelpful representation. For this assignment, you will be providing Maple with numerical values for the initial conditions. The four-step process for this is:
- Set up equations for the DC steady-state values in terms of the sources and elements
eqn1 := (vC(0)-vsDC)/R1 + vC(0)/R2 = 0
- Put those equations in a list:
eqns := [eqn1]
- Solve those equations:
sssoln := solve(eqns, [vC(0)])
- Substitute numbers into those solutions and de-bracket the list for use later:
numsssoln := subs(vals, sssoln)[][]
At the end of this step, there will be an un-bracketed set of equations storing the values of the variables at time 0.
Differential Equations
Next set up the differential equations, generate a single list of the differential equations with numerical values substituted in for the elements and sources, and solve. This is a three step process: define the equations:
deqn1 := (v__C(t)-v__S(t))/R__1+v__C(t)/R__2+C*(diff(v__C(t), t)) = 0
then define and substitute in the element and source values to your initial value solutions and your differential equations:
numeqn := subs(vals, {deqn1, sssoln[][]})
The end result will be a set of equations with numbers instead of symbols (except for the variables of interest). Now solve the equations:
soln := dsolve(numeqn, [v__C(t)])
You may want to look at a simplified version of the solution by first converting it to cos, sin, and exponentials (in case there are hyperbolic trig functions) and allowing Maple to expand and combine terms, then round off to four significant figures:
evalf[4](combine(expand(convert(soln, expsincos))))
Note that in some cases the results of the differential equation are, frankly, ugly. Sometimes, telling Maple to solve using the Laplace method comes up with a more compact answer:
soln := dsolve(numeqn, [v__C(t)], method=laplace): evalf[4](combine(expand(convert(soln, expsincos))))
Other times, neither Maple's default method nor Laplace have a ``nice answer; in those cases, simply put a colon at the end of the line to suppress the output and forget about the simplify line:
soln := dsolve(numeqn, [v__C(t)]):
In those cases, you will want to focus more on the plot than the analytical solution.
Plotting
Plotting can sometimes be a little more complicated than it seems - much of the
time, round-off errors will cause solutions that have tiny vestigial
imaginary values. To eliminate this, you can have Maple map the
real part of the solution vector. That is:
plot(map(Re, subs(soln, [v__C(t)])), t = 0 .. 10, labels = [typeset(t, ", s"), typeset(v__C(t), ", V")])