Difference between revisions of "Python:Logical Masks"
| Line 10: | Line 10: | ||
==Important Notes== | ==Important Notes== | ||
| − | |||
| − | |||
* All of the example codes assume you have already run (or have included in your script) | * All of the example codes assume you have already run (or have included in your script) | ||
<source lang=python> | <source lang=python> | ||
| Line 60: | Line 58: | ||
GPA = MaskForA*FunctionForA | GPA = MaskForA*FunctionForA | ||
</source> | </source> | ||
| − | At the end of this | + | At the end of this script, the <code>GPA</code> variable will contain a 4 |
wherever the logical mask <code>MaskForA</code> was True and it will contain a | wherever the logical mask <code>MaskForA</code> was True and it will contain a | ||
0 wherever the logical mask was False. All that is required is to | 0 wherever the logical mask was False. All that is required is to | ||
| − | extend this to the rest of the possible GPA's - the full code is in the section below, | + | extend this to the rest of the possible GPA's - the full code for a function is in the section below, |
| − | along with an image of the graph it will create. Note the use of | + | along with an image of the graph it will create. Note the use of an outer set of parentheses |
| − | + | to write the commands in the same visual way the function definition is written - | |
this is not required, but does make the code easier to interpret. | this is not required, but does make the code easier to interpret. | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
====Code and Graph==== | ====Code and Graph==== | ||
<source lang="python"> | <source lang="python"> | ||
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | + | ||
| − | + | ||
| − | + | def num_to_gpa(grade): | |
| − | + | out = ( | |
| − | + | (grade >= 90) * (4) | |
| − | + | + ((80 <= grade) & (grade < 90)) * (3) | |
| − | + | + ((70 <= grade) & (grade < 80)) * (2) | |
| − | + | + ((60 <= grade) & (grade < 70)) * (1) | |
| − | + | + (grade < 60) * (0) | |
| − | GPA = | + | ) |
| − | + | return out | |
| − | + | ||
| − | + | ||
| − | + | if __name__ == "__main__": | |
| − | + | ||
| − | + | grades = np.linspace(0, 100, 1000) | |
| − | + | GPA = num_to_gpa(grades) | |
| − | + | ||
| − | + | fig = plt.figure(num=1, clear=True) | |
| − | + | ax = fig.add_subplot(1, 1, 1) | |
| + | ax.plot(Grade, GPA) | ||
| + | ax.set( | ||
| + | xlabel="Numerical Grade", ylabel="GPA", | ||
| + | title="GPA vs. Grade for EGR 103L (mrg)" | ||
| + | ) | ||
| + | fig.tight_layout() | ||
| + | fig.savefig("GPAPlot.png") | ||
</source> | </source> | ||
<center> | <center> | ||
| Line 100: | Line 102: | ||
</center> | </center> | ||
| − | For a further explanation, look at the following | + | For a further explanation, look at the following script. It investigates the individual masks for each grade for an array containing eight different grades: |
| − | |||
<source lang="python"> | <source lang="python"> | ||
ClassGrades = np.array([95, 70, 68, 38, 94, 84, 92, 87]) | ClassGrades = np.array([95, 70, 68, 38, 94, 84, 92, 87]) | ||
MaskForA = ClassGrades>=90 | MaskForA = ClassGrades>=90 | ||
| − | |||
MaskForB = (80<=ClassGrades) & (ClassGrades<90) | MaskForB = (80<=ClassGrades) & (ClassGrades<90) | ||
| − | |||
MaskForC = (70<=ClassGrades) & (ClassGrades<80) | MaskForC = (70<=ClassGrades) & (ClassGrades<80) | ||
| − | |||
MaskForD = (60<=ClassGrades) & (ClassGrades<70) | MaskForD = (60<=ClassGrades) & (ClassGrades<70) | ||
| − | |||
MaskForF = ClassGrades<60 | MaskForF = ClassGrades<60 | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</source> | </source> | ||
| − | The masks now | + | The masks now look like: |
<source lang="python"> | <source lang="python"> | ||
MaskForA: array([ True, False, False, False, True, False, True, False]) | MaskForA: array([ True, False, False, False, True, False, True, False]) | ||
| Line 131: | Line 121: | ||
</source> | </source> | ||
| − | and the | + | and the products of each of the masks with each of the relevant GPA values would produce: |
<source lang="python"> | <source lang="python"> | ||
| Line 146: | Line 136: | ||
GPA: array([4, 2, 1, 0, 4, 3, 4, 3]) | GPA: array([4, 2, 1, 0, 4, 3, 4, 3]) | ||
</source> | </source> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Non-constant Piecewise Functions == | == Non-constant Piecewise Functions == | ||
| Line 180: | Line 157: | ||
which, for integers -2 through 12 can be calculated and graphed: | which, for integers -2 through 12 can be calculated and graphed: | ||
====Code and Graph==== | ====Code and Graph==== | ||
| + | |||
<source lang="python"> | <source lang="python"> | ||
| − | + | import numpy as np | |
| − | + | import matplotlib.pyplot as plt | |
| − | + | ||
| − | + | def fun(x): | |
| − | + | out = ( | |
| − | + | (x<0) * (0) + | |
| − | + | ((0<=x) & (x<5)) * (x) + | |
| − | + | ((5<=x) & (x<10)) * (5) + | |
| − | + | (x>=10) * (2*x-15)) | |
| − | + | return out | |
| − | + | ||
| − | + | if __name__ == "__main__": | |
| − | + | ||
| − | + | xvals = np.arange(-2, 13) | |
| − | + | yvals = fun(xvals) | |
| − | + | fig = plt.figure(num=1, clear=True) | |
| − | + | ax = fig.add_subplot(1, 1, 1) | |
| − | + | ax.stem(xvals, yvals) | |
| − | + | ax.set(xlabel='x', ylabel='f(x)', | |
| + | title ='Piecewise Function (NetID)') | ||
| + | fig.tight_layout() | ||
| + | fig.savefig('PFunction.png') | ||
</source> | </source> | ||
<center> | <center> | ||
| Line 205: | Line 186: | ||
</center> | </center> | ||
| − | Several of | + | Several of the intermediate results are presented below. Note that the spacing |
in this document is set to make it easier to see which elements in one variable are | in this document is set to make it easier to see which elements in one variable are | ||
paired up with equivalent elements in another variable (for example, | paired up with equivalent elements in another variable (for example, | ||
| − | to determine the element-multiplication of <code> | + | to determine the element-multiplication of <code>Mask 2</code> and <code>Function 2</code>). |
| − | + | Note that the masks are shown below as arrays with 1 representing True and 0 | |
representing False in order to save space: | representing False in order to save space: | ||
<source lang="python"> | <source lang="python"> | ||
| − | + | (x>0) * 1: array([1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) | |
| − | + | ((0<=x) & (x<5)) * (x) * 1: array([0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0]) | |
| − | + | ((5<=x) & (x<10)) * 1: array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0]) | |
| − | + | (x>=10) * 1: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1]) | |
</source> | </source> | ||
Notice how the masks end up spanning the entire domain of <math>x</math> without | Notice how the masks end up spanning the entire domain of <math>x</math> without | ||
| Line 221: | Line 202: | ||
domain, are: | domain, are: | ||
<source lang="python"> | <source lang="python"> | ||
| − | + | Function 1: 0 | |
| − | + | Function 2: array([-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]) | |
| − | + | Function 3: 5 | |
| − | + | Function 4: array([-19, -17, -15, -13, -11, -9, -7, -5, -3, -1, 1, 3, 5, 7, 9]) | |
</source> | </source> | ||
The individual products of the masks and the functions give: | The individual products of the masks and the functions give: | ||
<source lang="python"> | <source lang="python"> | ||
| − | + | Mask 1 *Function 1: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) | |
| − | + | Mask 2 *Function 2: array([0, 0, 0, 1, 2, 3, 4, 0, 0, 0, 0, 0, 0, 0, 0]) | |
| − | + | Mask 3 *Function 3: array([0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 5, 5, 0, 0, 0]) | |
| − | + | Mask 4 *Function 4: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 7, 9]) | |
</source> | </source> | ||
Finally, when these are all added together, none of the individual | Finally, when these are all added together, none of the individual | ||
| Line 239: | Line 220: | ||
f: array([0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 5, 7, 9]) | f: array([0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 5, 7, 9]) | ||
</source> | </source> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===Example 2 - Acceleration Due To Gravity === | ===Example 2 - Acceleration Due To Gravity === | ||
Revision as of 15:04, 17 February 2021
Contents
Introduction
Many times, you will see functions that are written in some kind of piecewise fashion. That is, depending upon that value of the input argument, the output argument may be calculated in one of several different ways. In these cases, you can use Python and NumPy's logical and relational arguments to create logical masks - arrays containing either 0's or 1's - to help determine the appropriate calculation to perform to determine the values in an array.
Important Notes
- All of the example codes assume you have already run (or have included in your script)
import math as m
import numpy as np
import matplotlib.pyplot as plt
Piecewise Constant
Sometimes, piecewise functions are broken up into several regions, with each region being defined by a single constant. These are called piecewise constant functions and can be easily generated in Python with NumPy.
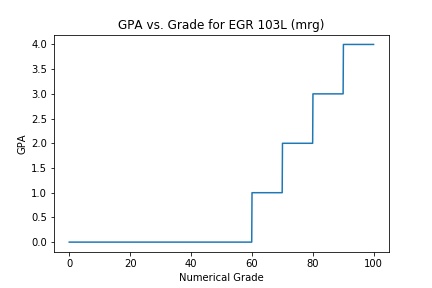
Example - GPA Calculation
Take for example GPA as a function of numerical grade (assume \(\pm\)do not exist for the moment...). The mathematical statement of GPA might be:
\( \mbox{GPA}(\mbox{Grade})=\left\{ \begin{array}{rl} \mbox{Grade}\geq 90~~~ & 4\\ 80\leq\mbox{Grade} ~\And~ \mbox{Grade}<90~~~ & 3\\ 70\leq\mbox{Grade} ~\And~ \mbox{Grade}<80~~~ & 2\\ 60\leq\mbox{Grade} ~\And~ \mbox{Grade}<70~~~ & 1\\ \mbox{Grade}<60~~~ & 0 \end{array} \right. \)
If you want to write this table as a function that can accept multiple
inputs at once, you really should not use an if-tree
(because if-trees can only run one program segment for the entire matrix) or a
for loop (because for loops are slower and more complex
for this particular situation).
Instead, use NumPy's ability to create logical masks. Look
at the following code:
Grade=np.linspace(0, 100, 1000)
MaskForA = Grade>=90
The variable MaskForA will be the same size of the Grade
variable, and will contain only True and False values. Given that, you can use
this in conjunction with the function for an "A" grade to start
building the GPA variable if you recall that True evaluates to 1 and False to 0:
Grade=np.linspace(0, 100, 1000)
MaskForA = Grade>=90
FunctionForA = 4
GPA = MaskForA*FunctionForA
At the end of this script, the GPA variable will contain a 4
wherever the logical mask MaskForA was True and it will contain a
0 wherever the logical mask was False. All that is required is to
extend this to the rest of the possible GPA's - the full code for a function is in the section below,
along with an image of the graph it will create. Note the use of an outer set of parentheses
to write the commands in the same visual way the function definition is written -
this is not required, but does make the code easier to interpret.
Code and Graph
import numpy as np
import matplotlib.pyplot as plt
def num_to_gpa(grade):
out = (
(grade >= 90) * (4)
+ ((80 <= grade) & (grade < 90)) * (3)
+ ((70 <= grade) & (grade < 80)) * (2)
+ ((60 <= grade) & (grade < 70)) * (1)
+ (grade < 60) * (0)
)
return out
if __name__ == "__main__":
grades = np.linspace(0, 100, 1000)
GPA = num_to_gpa(grades)
fig = plt.figure(num=1, clear=True)
ax = fig.add_subplot(1, 1, 1)
ax.plot(Grade, GPA)
ax.set(
xlabel="Numerical Grade", ylabel="GPA",
title="GPA vs. Grade for EGR 103L (mrg)"
)
fig.tight_layout()
fig.savefig("GPAPlot.png")
For a further explanation, look at the following script. It investigates the individual masks for each grade for an array containing eight different grades:
ClassGrades = np.array([95, 70, 68, 38, 94, 84, 92, 87])
MaskForA = ClassGrades>=90
MaskForB = (80<=ClassGrades) & (ClassGrades<90)
MaskForC = (70<=ClassGrades) & (ClassGrades<80)
MaskForD = (60<=ClassGrades) & (ClassGrades<70)
MaskForF = ClassGrades<60
The masks now look like:
MaskForA: array([ True, False, False, False, True, False, True, False])
MaskForB: array([False, False, False, False, False, True, False, True])
MaskForC: array([False, True, False, False, False, False, False, False])
MaskForD: array([False, False, True, False, False, False, False, False])
MaskForF: array([False, False, False, True, False, False, False, False])
and the products of each of the masks with each of the relevant GPA values would produce:
MaskForA*FunctionForA: array([4, 0, 0, 0, 4, 0, 4, 0])
MaskForB*FunctionForB: array([0, 0, 0, 0, 0, 3, 0, 3])
MaskForC*FunctionForC: array([0, 2, 0, 0, 0, 0, 0, 0])
MaskForD*FunctionForD: array([0, 0, 1, 0, 0, 0, 0, 0])
MaskForF*FunctionForF: array([0, 0, 0, 0, 0, 0, 0, 0])
These five matrices are added together to give:
GPA: array([4, 2, 1, 0, 4, 3, 4, 3])
Non-constant Piecewise Functions
Sometimes, piecewise functions are defined as following different formulas involving the independent variable over a range of inputs rather than being piece-wise constant.
Example 1 - Discrete Function
For example, the expression:
\( f(x)=\left\{ \begin{array}{rl} x<0 & 0\\ 0\leq x<5 & x\\ 5\leq x<10 & 5\\ x\geq 10 & 2x-15 \end{array} \right. \)
which, for integers -2 through 12 can be calculated and graphed:
Code and Graph
import numpy as np
import matplotlib.pyplot as plt
def fun(x):
out = (
(x<0) * (0) +
((0<=x) & (x<5)) * (x) +
((5<=x) & (x<10)) * (5) +
(x>=10) * (2*x-15))
return out
if __name__ == "__main__":
xvals = np.arange(-2, 13)
yvals = fun(xvals)
fig = plt.figure(num=1, clear=True)
ax = fig.add_subplot(1, 1, 1)
ax.stem(xvals, yvals)
ax.set(xlabel='x', ylabel='f(x)',
title ='Piecewise Function (NetID)')
fig.tight_layout()
fig.savefig('PFunction.png')
Several of the intermediate results are presented below. Note that the spacing
in this document is set to make it easier to see which elements in one variable are
paired up with equivalent elements in another variable (for example,
to determine the element-multiplication of Mask 2 and Function 2).
Note that the masks are shown below as arrays with 1 representing True and 0
representing False in order to save space:
(x>0) * 1: array([1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
((0<=x) & (x<5)) * (x) * 1: array([0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0])
((5<=x) & (x<10)) * 1: array([0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0])
(x>=10) * 1: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1])
Notice how the masks end up spanning the entire domain of \(x\) without overlapping. The functions - as calculated over the entire domain, are:
Function 1: 0
Function 2: array([-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
Function 3: 5
Function 4: array([-19, -17, -15, -13, -11, -9, -7, -5, -3, -1, 1, 3, 5, 7, 9])
The individual products of the masks and the functions give:
Mask 1 *Function 1: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
Mask 2 *Function 2: array([0, 0, 0, 1, 2, 3, 4, 0, 0, 0, 0, 0, 0, 0, 0])
Mask 3 *Function 3: array([0, 0, 0, 0, 0, 0, 0, 5, 5, 5, 5, 5, 0, 0, 0])
Mask 4 *Function 4: array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5, 7, 9])
Finally, when these are all added together, none of the individual products interfere with each other, so:
f: array([0, 0, 0, 1, 2, 3, 4, 5, 5, 5, 5, 5, 5, 7, 9])
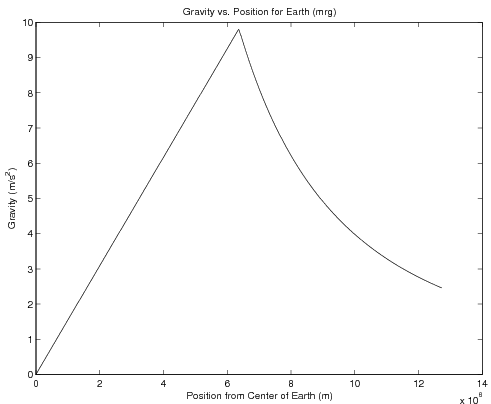
Example 2 - Acceleration Due To Gravity
The following example determines the acceleration due to gravity for a sphere a particular distance away from the center of a sphere of constant density \(\rho\) and radius R. The formula changes depending on whether you are inside the sphere's surface or not. That is:
\( \mbox{Gravity}(r)= \left\{ \begin{array}{lr} r<=R & \frac{4}{3}\pi G\rho r\\ r>R & \frac{4}{3}\pi G \rho\frac{R^3}{r^2} \end{array} \right. \)
You can use the same method as the example above, making sure to calculate the values of the function rather than simply using constants. The following code and graph demonstrate:
Code and Graph
G = 6.67e-11
rho = 5515
R = 6371e3
Position = np.linspace(0.1, 2*R, 1000)
MaskForInside = Position<=R
FunctionForInside = 4/3*m.pi*G*rho*Position
MaskForOutside = Position>R
FunctionForOutside = 4/3*m.pi*G*rho*R**3/Position**2
Gravity = \
MaskForInside*FunctionForInside + \
MaskForOutside*FunctionForOutside
plt.plot(Position, Gravity, 'k-');
plt.xlabel('Position from Center of Earth ($m$)');
plt.ylabel('Gravity ($m/s^2$)');
plt.title('Gravity vs. Position for Earth (mrg)');
plt.savefig('GravityPlot.png')
Using Logical Masks in Functions
Any of these tasks can be done using functions. For example, you could use a function in the script to compute the gravity - in this case G could be defined in the function, the density and radius of the planet in question could be passed along (with Earth value as the default, because, astronomical narcissism), and the rest of the work could be in the script itself.
def grav_fun(r, rho=5515, R=6371e3):
# Note: defaults to Earth
G = 6.67e-11
return (r<=R) * (4/3*m.pi*G*rho*r) + \
(r>R) * (4/3*m.pi*G*rho*R**3/r**2)
Position = np.linspace(0.1, 2*R, 1000)
plt.plot(Position, grav_fun(Position), 'k-')
plt.xlabel('Position from Center of Earth (m)')
plt.ylabel('Gravity (m/s^2)')
plt.title('Gravity vs. Position for Earth (mrg)')
plt.savefig('GravityPlot.png')
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.