Singularity Functions

Singularity Functions are a class of functions that - you guessed it - contain singularities. One notation for a singularity function is given as adapted from p. 77 Chapra

\( \begin{align} <x-a>^n&= \left\{ \begin{array}{cc} 0, & x\leq a\\ (x-a)^n, & x>a \end{array} \right. \end{align} \)

Note that this definition is only useful when \(n\geq 0\). Negative values of \(n\) are used to denote the impulse function (when \(n=-1\)) or its derivatives. Also note that it is common to leave the singularity undefined when \(n=0\) and \(x=a\). That is to say, a fuller definition of the singularity function might be:

\( \begin{align} <x-a>^n&= \left\{ \begin{array}{ccc} \delta^{(1-n)}(x), & ~ & n<0\\ 0, & x<a & ~\\ \mbox{Undefined}, & x=a & n=0\\ 1, & x>a & n=0\\ (x-a)^n, & x\geq a & n>0\\ \end{array} \right. \end{align} \)

where the delta function \(\delta(x)\) and its derivatives will be defined below.

Alternate Names for \(n\geq 0\)

Graph of Unit Singularity Functions

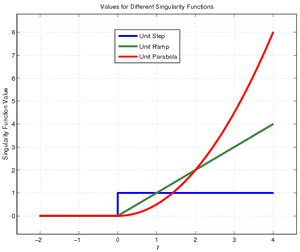
In courses such as ECE 54 and EGR 119, alternate names are given to different non-negative powers of the singularity function. Furthermore, singularity functions are generally written as functions of time rather than space, so:

\( \begin{align} \begin{array}{|c|c|c|}\hline \mbox{Singularity Function} & \mbox{Name} & \mbox{Alternate Symbol} \\ \hline \hline <t-a>^0 & \mbox{unit step function} & u(t) \\ \hline <t-a>^1 & \mbox{unit ramp function} & r(t)=t~u(t) \\ \hline \frac{1}{2}<t-a>^2 & \mbox{unit parabola function} & p(t)=\frac{1}{2}t^2~u(t) \\ \hline \end{array} \end{align} \)

For the last entry, you may be tempted to ask, "How is that the unit parabola?" The simplest explanation is that the unit ramp is the integral of the unit step, and the unit parabola is the integral of the unit parabola.

Derivation of Impulse Functions

You can also take derivatives of the singularity functions. For \(n>0\), this is quite easy as the unit ramp and above are continuous. The difficulty comes in taking the derivative of the \(<t-a>^0\) case. Mathematically, call the derivative of the unit step function \(\delta(t)\); you can then find

\( \delta(t)=\begin{align} \frac{d}{dt}u(t)&= \left\{ \begin{array}{cc} 0, & t\neq 0\\ \infty, & t=0 \end{array} \right. \end{align} \)

But how large is that infinity? The answer comes in integrating this "delta function" (also known as the "impulse function"):

\( \begin{align} u(t)&=\int_{-\infty}^t\delta(\tau)~d\tau \end{align} \)

and by definition,

\( \begin{align} u(t)&= \left\{ \begin{array}{cc} 0, & t< 0\\ 1, & t>0 \end{array} \right. \end{align} \)

meaning

\( \begin{align} \int_{-\infty}^t\delta(\tau)~d\tau &= \left\{ \begin{array}{cc} 0, & t< 0\\ 1, & t>0 \end{array} \right. \end{align} \)

In other words (well...in words) the total area is 0 when integrating between negative infinity and just before 0 and the total area is 1 when integrating between negative infinity and anything positive. That must mean, at exactly \(t=0\), \(\delta(t)\) has an area of 1 while for all other times, it has an area of 0. That is to say,

\( \begin{align} \delta(t)&= \left\{ \begin{array}{cc} 0, & t\neq 0\\ \mbox{Area of 1}, & t=0 \end{array} \right. \end{align} \)

Questions

Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.