Difference between revisions of "MATLAB:Fzero"
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The <code>fzero</code> command in MATLAB can be used to find the value of a single parameter of a multivariable function that will set the function equal to zero (if such a value exists). The command can ''only'' find one root at a time, and can only find roots in one variable at a time. There are several different ways to present <code>fzero</code> with the specific function and variable. | + | The <code>fzero</code> command in MATLAB can be used to find the value of a single parameter of a multivariable function that will set the function equal to zero (if such a value exists). The command can ''only'' find one root at a time, and can only find roots in one variable at a time. There are several different ways to present <code>fzero</code> with the specific function and variable. In addition to the examples below, there is another page with more examples at [[MATLAB:Fzero/Examples]]. |
== Examples == | == Examples == | ||
| Line 161: | Line 161: | ||
Now, <code>zVals</code> contains the values of <math>z</math> that will make the function equal to zero for the corresponding values of <math>x</math> in the <code>xVals</code> matrix. The plot is shown at right. You can prove to yourself that this is correct by re-arranging the equation <math>f=0</math> to note that <math>z=-\cos(x)-\sin(y)</math> and, if <math>y=\pi</math>, <math>z=-\cos(x)</math>. | Now, <code>zVals</code> contains the values of <math>z</math> that will make the function equal to zero for the corresponding values of <math>x</math> in the <code>xVals</code> matrix. The plot is shown at right. You can prove to yourself that this is correct by re-arranging the equation <math>f=0</math> to note that <math>z=-\cos(x)-\sin(y)</math> and, if <math>y=\pi</math>, <math>z=-\cos(x)</math>. | ||
==== Two Parameters ==== | ==== Two Parameters ==== | ||
| − | The next logical expansion is to allow both <math>x</math> and <math>y</math> to change. There are two fundamentally different ways to approach this problem - either <math>x</math> and <math>y</math> can be represented by one-dimensional vectors and accessed as such or they can be created using a <code>meshgrid</code> structure. The latter will take up more memory, but at least all the matrices will be the same size and all entries can be accessed using the same row and column notation. As help for how you might set up such a problem, imagine that you want to find the | + | The next logical expansion is to allow both <math>x</math> and <math>y</math> to change. There are two fundamentally different ways to approach this problem - either <math>x</math> and <math>y</math> can be represented by one-dimensional vectors and accessed as such or they can be created using a <code>meshgrid</code> structure. The latter will take up more memory, but at least all the matrices will be the same size and all entries can be accessed using the same row and column notation. As help for how you might set up such a problem, imagine that you want to find the roots of some function <math>f(\alpha, \beta, \gamma)</math> - and you know <math>\alpha</math> goes from 1 to 11 by 2 and <math>\beta</math> goes from 10 to 100 by 10. Assuming you call the first variable <code>Alpha</code> and the second variable <code>Beta</code>, you can create a matrix <code>Gamma</code> with the code as follows: |
<source lang=matlab> | <source lang=matlab> | ||
[Alpha, Beta] = meshgrid(1:2:11, 10:10:100); | [Alpha, Beta] = meshgrid(1:2:11, 10:10:100); | ||
[Rows, Cols] = size(Alpha) | [Rows, Cols] = size(Alpha) | ||
| + | Gamma = zeros(Rows, Cols); | ||
for R = 1:Rows | for R = 1:Rows | ||
for C = 1:Cols | for C = 1:Cols | ||
| − | Gamma(R, C) = Alpha(R, C) | + | Gamma(R, C) = fzero(@(GammaDummy} f(Alpha(R, C), Beta(R, C), GammaDummy), <initial guess or bracket>) |
end | end | ||
end | end | ||
| Line 176: | Line 177: | ||
meshc(Alpha, Beta, Gamma) | meshc(Alpha, Beta, Gamma) | ||
</source> | </source> | ||
| − | + | ||
| − | + | Since <code>fzero</code> can only solve one value at a time, the double for loop is a useful way of sweeping through each possible set of parameters and storing the results in an organization structure that will lend itself to surface plotting later. The above is a demonstration of how a double loop might work. Note also that <code>beta</code> and </code>gamma</code> are built-in MATLAB functions - thus the use of capitals to avoid redefining built-in functions! | |
| − | |||
| − | |||
| − | |||
== Questions == | == Questions == | ||
| Line 191: | Line 189: | ||
{{Template:Protected Class Document}} | {{Template:Protected Class Document}} | ||
| + | |||
| + | [[Category:EGR 103]] | ||
Latest revision as of 22:09, 1 October 2012
The fzero command in MATLAB can be used to find the value of a single parameter of a multivariable function that will set the function equal to zero (if such a value exists). The command can only find one root at a time, and can only find roots in one variable at a time. There are several different ways to present fzero with the specific function and variable. In addition to the examples below, there is another page with more examples at MATLAB:Fzero/Examples.
Examples
Different Function Calls
Most General Case
The following examples show a method that will work regardless of how many input variables your function has or how you define your function - whether it is built-in, a variable containing an anonymous function, an anonymous function generated on the fly, or a .m file function. The paradigm is:
[ROOT, VAL_AT_ROOT] = fzero(@(DUMMY_VAR) FUNCTION_THING, INIT_STUFF, OPTIONS)
where
- ROOT is the calculated value of the requested variable when the function is 0
- VAL_AT_ROOT is the value of the function when substituting ROOT for the requested variable - nominally this is 0 but there may be roundoff issues to deal with
- DUMMY_VAR is the variable you want to use in this FUNCTION_THING to indicate which of the various inputs
fzerois allowed to alter - INIT_STUFF is either an initial guess or a valid initial bracket - note that
fzerocan only find one root at a time, so you cannot load this with several values and try to havefzerofind multiple results (for that, you need loops) - FUNCTION_THING can be a built-in function, the name of an anonymous function, the name of a .m file function, or a calculation - whatever it is that you are trying to set equal to zero; note that DUMMY_VAR must appear somewhere in this expression for
fzeroto be able to do anything - OPTIONS are...optional - the most common is the commandif you want to see the magic happen
optimset('Display', 'iter')
The example is based on wanting to determine roots of:
We will assume that two of the three variables (\(x\) and \(y\)) are known and that we want to find \(z\) given those values. We will further assume that \(x=1\) and \(y=\pi\). Finally, we will make an initial guess that \(z=12\).
Function on the Fly
If you only want to solve this problem once, and the calculation only requires one line of code, the process with the least "overhead" involves creating the function on the fly inside the fzero command. All you have to do is put your expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. The line:
[zValue, fValue] = fzero(@(zDummy) cos(1) + sin(pi) + zDummy, 12)
will produce
zValue =
-5.4030e-01
fValue =
0
A slightly "longer" version of this would have you pre-define the \(x\) and \(y\) variables first, then use the variables in the function definition: expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. The line:
x = 1;
y = pi;
[zValue, fValue] = fzero(@(zDummy) cos(x) + sin(y) + zDummy, 12)
This works the same as the previous example - recall that when anonymous functions are created, they can take "snapshots" of the workspace. In the case above, the FUNCTION_THING is able to "see" what the variables x and y contain.
Pre-Defined Functions
If you want to solve the same problem multiple times, perhaps by altering initial guesses or altering one or more of the constant parameters in the function, you should first define the function. If the expression can be calculated all on one line, you may choose to use a variable with an anonymous function - for example:
MyFun = @(xa, ya, za) cos(xa) + sin(ya) + za
On the other hand, if the expression is more complicated or if you just want to put it in a .m file, you can certainly do that as well. or example, instead of the MyFun variable above, you could write a MyFun.m file containing:
function out = MyFun(xb, yb, zb)
out = cos(xb) + sin(yb) + zb;
In either case, you would use fzero by properly building the FUNCTION_THING using the name of the function. As in the previous example, you can hard-code the values for the \(x\) and \(y\) values:
[zValue, fValue] = fzero(@(zDummy) MyFun(1, pi, zDummy), 12)
or you can use variables to transmit the information:
x = 1;
y = pi;
[zValue, fValue] = fzero(@(zDummy) MyFun(x, y, zDummy), 12)
In any event, note again that the FUNCTION_THING only has one unknown, and that unknown is named as the DUMMY_VAR.
Single-Variable Anonymous Functions
For single-variable anonymous functions, there is a slightly simpler way to run fzero - all you need to do is give the name of the variable to FUNCTION_THING rather than setting up the DUMMY_VAR. For example, to find the solution to \(x^2-\cos(x)=0\) with an initial guess of \(x=1\), you can set up an anonymous function for it as:
MyAnonCalc = @(x) x.^2-cos(x)
and then solve with:
[xValue, fValue] = fzero(MyAnonCalc, 1)
to get
xValue =
8.2413e-01
fValue =
-1.1102e-16
Single-Variable Built-in Functions and .m Functions
The following method works for both built-in single-input functions and .m file single-input functions (i.e. not variables containing anonymous functions). The first argument is the name of the function in single quotes and the second argument is the initial guess or initial bracket for the one variable of the function. For example, to find the solution to \(\cos(x)=0\) with an initial guess of \(x=1\), you can type
[xValue, fValue] = fzero('cos', 1)
and get
xValue =
1.5708e+00
fValue =
6.1232e-17
To find the solution for \(x\) values between 2 and 5 radians, you could type:
[xValue, fValue] = fzero('cos', [2 5])
and get
xValue =
4.7124e+00
fValue =
-1.8370e-16
If you have a .m file function of one variable, the process is the same. For example, to find a root of \(y=x^2-\cos(x)\) with an initial guess of 1, you could first create a .m file called MyCalc.m with:
function out = MyCalc(in)
out = in.^2 - cos(in);
then use fzero:
[xValue, fValue] = fzero('MyCalc', 1)
and get
xValue =
8.2413e-01
fValue =
-1.1102e-16
Changing "Constant" Parameters
In each of the examples above, there was only one variable that MATLAB had control over; everything else remained constant. Sometimes, there may be a function of multiple variables where you want to find the value of the root as a function of one or more parameters of the function. We will again use the example:
One Parameter
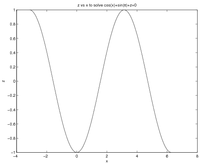
Now assume that we still set \(y=\pi\) but we want to calculate \(z\) values that make \(f(x,y,z)=0\) for a variety of \(x\) values. The fzero command can still only solve for a single set of parameters at a time, so you need to construct a loop that will substitute the appropriate \(x\) values into the function and then store the resulting \(z\) value. The following example code will do this for 200 values of \(x\) between \(-\pi\) and \(2\pi\). It is based on a variable called MyFun that stores the anonymous function, but it could just as well work with a .m file containing the same calculation. The example also assumes an initial guess of 12 for the \(z\) value.
MyFun = @(xa, ya, za) cos(xa) + sin(ya) + za
xVals = linspace(-pi, 2*pi, 200);
yVal = pi;
for k=1:length(xVals)
[zVals(k), fVals(k)] = fzero(@(zDummy) MyFun(xVals(k), yVal, zDummy), 12);
end
Now, zVals contains the values of \(z\) that will make the function equal to zero for the corresponding values of \(x\) in the xVals matrix. The plot is shown at right. You can prove to yourself that this is correct by re-arranging the equation \(f=0\) to note that \(z=-\cos(x)-\sin(y)\) and, if \(y=\pi\), \(z=-\cos(x)\).
Two Parameters
The next logical expansion is to allow both \(x\) and \(y\) to change. There are two fundamentally different ways to approach this problem - either \(x\) and \(y\) can be represented by one-dimensional vectors and accessed as such or they can be created using a meshgrid structure. The latter will take up more memory, but at least all the matrices will be the same size and all entries can be accessed using the same row and column notation. As help for how you might set up such a problem, imagine that you want to find the roots of some function \(f(\alpha, \beta, \gamma)\) - and you know \(\alpha\) goes from 1 to 11 by 2 and \(\beta\) goes from 10 to 100 by 10. Assuming you call the first variable Alpha and the second variable Beta, you can create a matrix Gamma with the code as follows:
[Alpha, Beta] = meshgrid(1:2:11, 10:10:100);
[Rows, Cols] = size(Alpha)
Gamma = zeros(Rows, Cols);
for R = 1:Rows
for C = 1:Cols
Gamma(R, C) = fzero(@(GammaDummy} f(Alpha(R, C), Beta(R, C), GammaDummy), <initial guess or bracket>)
end
end
You could then visualize it with a mesh with contours using:
meshc(Alpha, Beta, Gamma)
Since fzero can only solve one value at a time, the double for loop is a useful way of sweeping through each possible set of parameters and storing the results in an organization structure that will lend itself to surface plotting later. The above is a demonstration of how a double loop might work. Note also that beta and gamma are built-in MATLAB functions - thus the use of capitals to avoid redefining built-in functions!
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.
External Links
References