Difference between revisions of "Maple/Differential Equations/RC Example"
(→Further Examples) |
|||
| (27 intermediate revisions by the same user not shown) | |||
| Line 25: | Line 25: | ||
Using KCL at the top right node gives: | Using KCL at the top right node gives: | ||
<center><math> | <center><math> | ||
| − | \frac{v_C(0^-)- | + | \frac{v_C(0^-)-v_S}{R_1}+ |
\frac{v_C(0^-)}{R_2}=0\! | \frac{v_C(0^-)}{R_2}=0\! | ||
</math></center> | </math></center> | ||
| − | which can be solved to find the capacitor voltage at the time just before the source <math> | + | which can be solved to find the capacitor voltage at the time just before the source <math>v_S(t)</math> changes. |
== Model Equations for t>0 == | == Model Equations for t>0 == | ||
| Line 37: | Line 37: | ||
Using KCL at the top right node again gives: | Using KCL at the top right node again gives: | ||
<center><math> | <center><math> | ||
| − | \frac{v_C- | + | \frac{v_C(t)-v_S(t)}{R_1}+ |
| − | \frac{v_C}{R_2}+C\frac{dv_C}{dt}=0\! | + | \frac{v_C(t)}{R_2}+C\frac{dv_C(t)}{dt}=0\! |
</math></center> | </math></center> | ||
| − | |||
== Code == | == Code == | ||
| − | Now that the equations for DC steady state and for the differential model are known, you can write Maple code to solve for everything. | + | Now that the equations for DC steady state and for the differential model are known, you can write Maple code to solve for everything. A complete example of the code below is at the [https://maple.cloud/app/5138367069159424/RRCexample Maple Cloud] |
=== Preparing the Worksheet === | === Preparing the Worksheet === | ||
| Line 49: | Line 48: | ||
of the page. Also be sure that the first Maple command is <code>restart</code>. | of the page. Also be sure that the first Maple command is <code>restart</code>. | ||
| − | === | + | === Values === |
| − | + | Create a list of values for substitutions later. Note that there should probably be one variable for the DCSS steady-state analysis and another for the differential equations. In this case, <code>vsDC</code> will be the $$t<0$$ value and <code>vs(t)</code> will be for $$t\geq 0$$. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | will | ||
=== Initial Conditions From Steady-State === | === Initial Conditions From Steady-State === | ||
| − | While Maple can solve differential equations with symbolic initial | + | While Maple can solve differential equations with symbolic initial conditions and coefficients, most of the time this will result in a very unwieldy and unhelpful |
| − | conditions and coefficients, most of the | ||
| − | time this will result in a very unwieldy and unhelpful | ||
representation. For this assignment, you will be providing Maple with | representation. For this assignment, you will be providing Maple with | ||
| − | numerical values for the initial conditions. The | + | numerical values for the initial conditions. The four-step process |
| − | for this is | + | for this is: |
| − | of the sources and elements | + | * Set up equations for the DC steady-state values in terms of the sources and elements <syntaxhighlight>eqn1 := (vC(0)-vsDC)/R1 + vC(0)/R2 = 0</syntaxhighlight> |
| − | + | * Put those equations in a list:<syntaxhighlight>eqns := [eqn1]</syntaxhighlight> | |
| − | + | * Solve those equations:<syntaxhighlight>sssoln := solve(eqns, [vC(0)])</syntaxhighlight> | |
| − | + | * Substitute numbers into those solutions and de-bracket the list for use later:<syntaxhighlight>numsssoln := subs(vals, sssoln)[][]</syntaxhighlight> | |
| − | + | At the end of this step, there will be an un-bracketed set of equations storing the values of the variables at time 0. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | set of equations | ||
=== Differential Equations === | === Differential Equations === | ||
| − | + | For this assignment, you will also be providing substituting values into the differential equations - unlike the linear algebra equations above, however, you really need to make the substitutions before solving. The four-step process for this is: | |
| − | the | + | * Set up differential equations for $$t\geq 0$$: <syntaxhighlight>deqn1 := (vC(t) - vs(t))/R1 + (vC(t) + 0)/R2 + C*diff(vC(t), t) = 0</syntaxhighlight> |
| − | the | + | * Put those equations in a list:<syntaxhighlight>deqns := [deqn1]</syntaxhighlight> |
| − | equations: | + | * Substitute numbers into those equations and de-bracket for later:<syntaxhighlight>numdeqns := subs(vals, deqns)[]</syntaxhighlight> |
| − | + | * Solve those equations:<syntaxhighlight>dsoln := dsolve([numsssoln, numdeqns], [vC(t)])</syntaxhighlight> | |
| − | + | At the end of this step, there will be a solution or a collection of solutions for the variable or variables. If you want to see a version where numbers are converted to floating-point notation and rounded, include the code <syntaxhighlight>evalf[4](dsoln)</syntaxhighlight> | |
| − | + | ||
| − | + | === Plotting === | |
| − | |||
| − | |||
| − | |||
| − | Note that in | + | To make a plot, just substitute in your solution (or de-bracketed collection of solutions) into your variable of interest:: |
| + | <syntaxhighlight>plot(subs(dsoln, [vC(t)]), t = 0 .. 10, labels = [typeset(t, ", s"), typeset(v__C(t), ", V")]); | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | == Extra Steps == | ||
| + | Though not necessary for this particular example, there may be times when you may want to look at a simplified version of the solution by first converting it to | ||
| + | cos, sin, and exponentials (in case there are hyperbolic trig functions) and allowing | ||
| + | Maple to expand and combine terms, then round off to four significant figures:<syntaxhighlight> evalf[4](combine(expand(convert(dsoln, expsincos))))</syntaxhighlight> | ||
| + | |||
| + | Note that in some cases the results of the differential equation are, | ||
frankly, ugly. Sometimes, telling Maple to solve using the Laplace | frankly, ugly. Sometimes, telling Maple to solve using the Laplace | ||
method comes up with a more compact answer: | method comes up with a more compact answer: | ||
| − | + | <syntaxhighlight>dsoln := dsolve([numsssoln, numdeqns], [vC(t)], method=laplace) | |
| − | + | evalf[4](combine(expand(convert(dsoln, expsincos))))</syntaxhighlight> | |
| + | |||
Other times, neither Maple's default method nor Laplace have a | Other times, neither Maple's default method nor Laplace have a | ||
``nice'' answer; in those cases, simply put a colon at the end of the | ``nice'' answer; in those cases, simply put a colon at the end of the | ||
| − | line to suppress the output and forget about the simplify line: | + | line to suppress the output and forget about the simplify line:<syntaxhighlight>dsoln := dsolve([numsssoln, numdeqns], [vC(t)], method=laplace)</syntaxhighlight> |
| − | |||
In those cases, you will want to focus more on the plot than the | In those cases, you will want to focus more on the plot than the | ||
analytical solution. | analytical solution. | ||
| − | |||
Plotting can sometimes be a little more complicated than it seems - much of the | Plotting can sometimes be a little more complicated than it seems - much of the | ||
time, round-off errors will cause solutions that have tiny vestigial | time, round-off errors will cause solutions that have tiny vestigial | ||
imaginary values. To eliminate this, you can have Maple <code>map</code> the | imaginary values. To eliminate this, you can have Maple <code>map</code> the | ||
real part of the solution vector. That is: | real part of the solution vector. That is: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <syntaxhighlight>plot(map(Re, subs(dsoln, [vC(t)])), t = 0 .. 10, | |
| − | plot( | + | labels = [typeset(t, ", s"), typeset(vC(t), ", V")])</syntaxhighlight> |
| − | </ | ||
| − | + | == Further Examples == | |
| + | The following examples are from "Circuit Analysis and Design" by Ulaby, Maharbiz, and Furse - free download at: https://services.publishing.umich.edu/publications/ee/ | ||
| + | * CAD Example 0608 Underdamped - [https://maple.cloud/app/6507127311040512/CAD+Example+0608+Underdamped?key=EEA7F050169E4F8DAB8997F3C7ADFB66302825487348498ABD2BF536042C93C0 Maple Cloud Link] | ||
| + | * CAD Example 0610 Overdamped - [https://maple.cloud/app/5024665695289344/CAD+Example+0610+Overdamped?key=3347BAEC53D04D068EAB572DBA7E5425911676E5E122483984EFDBDBABB06EB8 Maple Cloud Link] | ||
Latest revision as of 14:09, 27 February 2024
Contents
Description
The following page will go through an example of using Maple's ability to work with differential equations to analyze a circuit that undergoes a change in source values. In this particular case, the independent source is given as a constant for all times before 0 sec, at which time it changes to a non-constant source. The source is connected to a network containing both resistors and a capacitor. While there are several ways to put all this work together in a Maple script, the following will provide a flexible framework for solving the equations and using substitution to determine a numerical list of initial conditions, substituting element values into the differential equations and putting them into a list, solving the differential equations, and finally plotting the results.
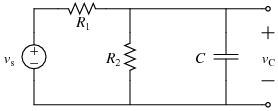
Circuit
For this demonstration code, the following circuit is used:
where \(R_1\)=20 k\(\Omega\), \(R_2\)=30 k\(\Omega\), \(C\)=50 \(\mu\)F, and \(v_s(t)\) changes from 5 V to 10 cos(8\(t\)) V when \(t=0\) s.
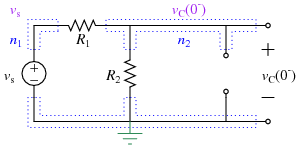
DC Steady-State Analysis
Assuming the circuit has been in place for a "long time" before \(t\)=0 sec, and given the topology of the circuit and the fact that the independent source is a constant for all times before 0 sec, you can use the DC steady-state equivalent for the circuit at \(t=0^-\) sec:
Using KCL at the top right node gives:
which can be solved to find the capacitor voltage at the time just before the source \(v_S(t)\) changes.
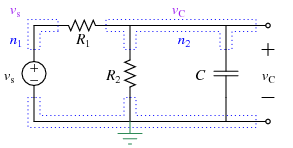
Model Equations for t>0
In general, after \(t\)=0 sec you can label the circuit as:
Using KCL at the top right node again gives:
Code
Now that the equations for DC steady state and for the differential model are known, you can write Maple code to solve for everything. A complete example of the code below is at the Maple Cloud
Preparing the Worksheet
Be sure that your name and the assignment show up as text at the top
of the page. Also be sure that the first Maple command is restart.
Values
Create a list of values for substitutions later. Note that there should probably be one variable for the DCSS steady-state analysis and another for the differential equations. In this case, vsDC will be the $$t<0$$ value and vs(t) will be for $$t\geq 0$$.
Initial Conditions From Steady-State
While Maple can solve differential equations with symbolic initial conditions and coefficients, most of the time this will result in a very unwieldy and unhelpful representation. For this assignment, you will be providing Maple with numerical values for the initial conditions. The four-step process for this is:
- Set up equations for the DC steady-state values in terms of the sources and elements
eqn1 := (vC(0)-vsDC)/R1 + vC(0)/R2 = 0
- Put those equations in a list:
eqns := [eqn1]
- Solve those equations:
sssoln := solve(eqns, [vC(0)])
- Substitute numbers into those solutions and de-bracket the list for use later:
numsssoln := subs(vals, sssoln)[][]
At the end of this step, there will be an un-bracketed set of equations storing the values of the variables at time 0.
Differential Equations
For this assignment, you will also be providing substituting values into the differential equations - unlike the linear algebra equations above, however, you really need to make the substitutions before solving. The four-step process for this is:
- Set up differential equations for $$t\geq 0$$:
deqn1 := (vC(t) - vs(t))/R1 + (vC(t) + 0)/R2 + C*diff(vC(t), t) = 0
- Put those equations in a list:
deqns := [deqn1]
- Substitute numbers into those equations and de-bracket for later:
numdeqns := subs(vals, deqns)[]
- Solve those equations:
dsoln := dsolve([numsssoln, numdeqns], [vC(t)])
At the end of this step, there will be a solution or a collection of solutions for the variable or variables. If you want to see a version where numbers are converted to floating-point notation and rounded, include the code
evalf[4](dsoln)Plotting
To make a plot, just substitute in your solution (or de-bracketed collection of solutions) into your variable of interest::
plot(subs(dsoln, [vC(t)]), t = 0 .. 10, labels = [typeset(t, ", s"), typeset(v__C(t), ", V")]);Extra Steps
Though not necessary for this particular example, there may be times when you may want to look at a simplified version of the solution by first converting it to cos, sin, and exponentials (in case there are hyperbolic trig functions) and allowing
Maple to expand and combine terms, then round off to four significant figures:
evalf[4](combine(expand(convert(dsoln, expsincos))))Note that in some cases the results of the differential equation are, frankly, ugly. Sometimes, telling Maple to solve using the Laplace method comes up with a more compact answer:
dsoln := dsolve([numsssoln, numdeqns], [vC(t)], method=laplace)
evalf[4](combine(expand(convert(dsoln, expsincos))))Other times, neither Maple's default method nor Laplace have a ``nice answer; in those cases, simply put a colon at the end of the
line to suppress the output and forget about the simplify line:
dsoln := dsolve([numsssoln, numdeqns], [vC(t)], method=laplace)In those cases, you will want to focus more on the plot than the analytical solution.
Plotting can sometimes be a little more complicated than it seems - much of the
time, round-off errors will cause solutions that have tiny vestigial
imaginary values. To eliminate this, you can have Maple map the
real part of the solution vector. That is:
plot(map(Re, subs(dsoln, [vC(t)])), t = 0 .. 10,
labels = [typeset(t, ", s"), typeset(vC(t), ", V")])Further Examples
The following examples are from "Circuit Analysis and Design" by Ulaby, Maharbiz, and Furse - free download at: https://services.publishing.umich.edu/publications/ee/
- CAD Example 0608 Underdamped - Maple Cloud Link
- CAD Example 0610 Overdamped - Maple Cloud Link