Difference between revisions of "MATLAB:Plotting"
| (5 intermediate revisions by the same user not shown) | |||
| Line 350: | Line 350: | ||
* Data points should be represented by symbols and model equations should be represented by lines. Be sure to use a legend to identify each item plotted if there are multiple data sets on the same graph. | * Data points should be represented by symbols and model equations should be represented by lines. Be sure to use a legend to identify each item plotted if there are multiple data sets on the same graph. | ||
* Typically, you will want to set the axis limits such that no data point is on the figure boundary. Certainly you do not want a line to be plotted on top of a figure boundary. After you make a plot, if there is a data point on an edge, look at the current axes and go out a little bit. Just make sure if you end up fundamentally changing your code that you adjust the axes accordingly. Alternately, you can use the [[#Keeping Data Off The Edge| gzoom]] function below to automatically expand the graph. | * Typically, you will want to set the axis limits such that no data point is on the figure boundary. Certainly you do not want a line to be plotted on top of a figure boundary. After you make a plot, if there is a data point on an edge, look at the current axes and go out a little bit. Just make sure if you end up fundamentally changing your code that you adjust the axes accordingly. Alternately, you can use the [[#Keeping Data Off The Edge| gzoom]] function below to automatically expand the graph. | ||
| + | * If you end up using the <code>hold on</code> command, you should only use it '''after''' the first plotting command is issued; if not, there are some parts of a typical plot that will not show up, such as the complete plot frame. | ||
== Keeping Data Off The Edge == | == Keeping Data Off The Edge == | ||
| Line 377: | Line 378: | ||
axis(f, [v + n*[-xr xr -yr yr]]); | axis(f, [v + n*[-xr xr -yr yr]]); | ||
</source> | </source> | ||
| + | |||
| + | Here's how the code works: | ||
| + | * If there is no argument to the function, the variable f grabs a handle for the current axes - that is to say, it will be a reference to wherever you last plotted. Also, n will be 0.1 which means the figure will bump out by 10% of the original size in each direction. | ||
| + | * If there is only one argument, the variable f still grabs the current axes but the function will use the first argument as the bump out factor. | ||
| + | * The v=axis line will figure out the left, right, bottom, and top limits of the current figure; this will be a 1x4 matrix | ||
| + | * xr takes the difference between the right and left values - think of this as the x range | ||
| + | * yr takes the difference between the top and bottom values - think of this as the y range | ||
| + | * The final line sets the new limits of the axis by taking the old limits (v) and then bumping them by n times the appropriate range (x or y). The left and right are bumped to the left and right, respectively, by n*xr while the bottom and top are bumped down and up, respectively, by n*yr. | ||
== Using Different Line Styles == | == Using Different Line Styles == | ||
| Line 386: | Line 395: | ||
y3 = x.^2; | y3 = x.^2; | ||
plot(x, y1, 'k-', x, y2, 'k--', x, y3, 'k:'); | plot(x, y1, 'k-', x, y2, 'k--', x, y3, 'k:'); | ||
| − | legend('y=x^{0.5}', 'y=x', 'y=x^2', | + | legend('y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best'); |
title('y=x^n for Three Values of n (mrg)'); | title('y=x^n for Three Values of n (mrg)'); | ||
xlabel('x'); | xlabel('x'); | ||
| Line 396: | Line 405: | ||
[[Image:CurvePlot.png]] | [[Image:CurvePlot.png]] | ||
</center> | </center> | ||
| − | Note the legend - the use of the final | + | Note the legend - the use of the final arguments ''' 'location', 'best' ''' will make MATLAB look for the best spot in the window for the legend - which is to say, somewhere ''not'' conflicting with any of the lines if at all possible. Also note that the text in the legend and in the title contains basic [[LaTeX]] code for obtaining the superscripts. |
== Using Different Point Styles == | == Using Different Point Styles == | ||
| Line 419: | Line 428: | ||
subplot(1,2,1) % left graph (ewwwwwww) | subplot(1,2,1) % left graph (ewwwwwww) | ||
plot(x, y1, 'k-s', x, y2, 'k-o', x, y3, 'k-p'); | plot(x, y1, 'k-s', x, y2, 'k-o', x, y3, 'k-p'); | ||
| − | legend('y=x^{0.5}', 'y=x', 'y=x^2', | + | legend('y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best'); |
title('y=x^n for Three Values of n (mrg)'); | title('y=x^n for Three Values of n (mrg)'); | ||
xlabel('x'); | xlabel('x'); | ||
| Line 434: | Line 443: | ||
x(Indices), y3(Indices), 'kp'); | x(Indices), y3(Indices), 'kp'); | ||
hold off | hold off | ||
| − | legend(PointPlot, 'y=x^{0.5}', 'y=x', 'y=x^2', | + | legend(PointPlot, 'y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best'); |
title('y=x^n for Three Values of n (mrg)'); | title('y=x^n for Three Values of n (mrg)'); | ||
xlabel('x'); | xlabel('x'); | ||
| Line 556: | Line 565: | ||
== Setting Limits and Tick Locations == | == Setting Limits and Tick Locations == | ||
| − | [[File:PalmFig050204plot.png|thumb| | + | [[File:PalmFig050204plot.png|thumb|300px]]You can set the specific limits and tick locations for a graph such that they will not change when you resize the figure window and so that they print exactly as you see on the screen. To do this, you will use the <code>set</code> command with some specific arguments. The following example is modified from Palm, Chapter 5.2, on page 231 to create the specific figure as shown in the book: |
<source lang=matlab> | <source lang=matlab> | ||
| Line 585: | Line 594: | ||
%% Print figure | %% Print figure | ||
print -deps PalmFig050204plot</source> | print -deps PalmFig050204plot</source> | ||
| + | |||
| + | [[File:PalmFig050204plot2.png|thumb|300px]] | ||
| + | You can also specify what goes at each tick mark - either by giving a vector of values or a cell array of strings. Changing the <code>set</code> command as given below produces the graph at right: | ||
| + | <source lang=matlab> | ||
| + | set(gca, 'XLim', [-1 6], 'YLim', [-1 7],... | ||
| + | 'XTick', -1:1:6, 'YTick', -1:1:7,... | ||
| + | 'XTickLabel',... | ||
| + | {'eight', 'things', 'must', 'go', 'in', 'here', 'to', 'work'}, ... | ||
| + | 'YTickLabel', ... | ||
| + | roundn(linspace(pi, 2*pi, 9), -2)) | ||
| + | </source> | ||
| + | where the <code>round(x,n)</code> command rounds <math>x</math> to the nearest <math>10^n</math>. | ||
| + | |||
== Questions == | == Questions == | ||
{{Questions}} | {{Questions}} | ||
Latest revision as of 01:19, 28 March 2018
This page will primarily go over some examples of different ways to plot data sets.
Contents
Introduction
The following introduction comes from "Making and Printing Plots in MATLAB," which was formerly an appendix to the EGR 103 lab manual. Information contained within this particular section may be modified or move as deemed appropriate.
The plot Function
The plot function is used to plot sets of data on a 2-D grid.
What follows comes from MATLAB's help function in MATLAB R2009a[1] (some
paragraphs have been snipped out). The line styles, symbols, and colors are formatted as a clearer table.
PLOT Linear plot.
PLOT(X,Y) plots vector Y versus vector X. If X or Y is a matrix,
then the vector is plotted versus the rows or columns of the matrix,
whichever line up. If X is a scalar and Y is a vector, disconnected
line objects are created and plotted as discrete points vertically at
X.
PLOT(Y) plots the columns of Y versus their index.
If Y is complex, PLOT(Y) is equivalent to PLOT(real(Y),imag(Y)).
In all other uses of PLOT, the imaginary part is ignored.
Various line types, plot symbols and colors may be obtained with
PLOT(X,Y,S) where S is a character string made from one element
from any or all the following 3 columns:
|
|
|
(continued)
For example, PLOT(X,Y,'c+:') plots a cyan dotted line with a plus
at each data point; PLOT(X,Y,'bd') plots blue diamond at each data
point but does not draw any line.
PLOT(X1,Y1,S1,X2,Y2,S2,X3,Y3,S3,...) combines the plots defined by
the (X,Y,S) triples, where the X's and Y's are vectors or matrices
and the S's are strings.
For example, PLOT(X,Y,'y-',X,Y,'go') plots the data twice, with a
solid yellow line interpolating green circles at the data points.
The PLOT command, if no color is specified, makes automatic use of
the colors specified by the axes ColorOrder property. The default
ColorOrder is listed in the table above for color systems where the
default is blue for one line, and for multiple lines, to cycle
through the first six colors in the table. For monochrome systems,
PLOT cycles over the axes LineStyleOrder property.
If you do not specify a marker type, PLOT uses no marker.
If you do not specify a line style, PLOT uses a solid line.
% snip
The X,Y pairs, or X,Y,S triples, can be followed by
parameter/value pairs to specify additional properties
of the lines. For example, PLOT(X,Y,'LineWidth',2,'Color',[.6 0 0])
will create a plot with a dark red line width of 2 points.
The subplot Function
The subplot function is used to plot multiple plot windows
within the same figure.
What follows comes from MATLAB's help function in MATLAB R2009a[2] (some
paragraphs have been snipped out).
SUBPLOT Create axes in tiled positions.
H = SUBPLOT(m,n,p), or SUBPLOT(mnp), breaks the Figure window
into an m-by-n matrix of small axes, selects the p-th axes for
for the current plot, and returns the axis handle. The axes
are counted along the top row of the Figure window, then the
second row, etc. For example,
SUBPLOT(2,1,1), PLOT(income)
SUBPLOT(2,1,2), PLOT(outgo)
plots income on the top half of the window and outgo on the
bottom half. If the CurrentAxes is nested in a uipanel the
panel is used as the parent for the subplot instead of the
current figure.
SUBPLOT(m,n,p), if the axis already exists, makes it current.
SUBPLOT(m,n,p,'replace'), if the axis already exists, deletes it and
creates a new axis.
SUBPLOT(m,n,p,'align') places the axes so that the plot boxes
are aligned instead of preventing the labels and ticks from
overlapping.
SUBPLOT(m,n,P), where P is a vector, specifies an axes position
that covers all the subplot positions listed in P.
SUBPLOT(H), where H is an axis handle, is another way of making
an axis current for subsequent plotting commands.
SUBPLOT('position',[left bottom width height]) creates an
axis at the specified position in normalized coordinates (in
in the range from 0.0 to 1.0).
SUBPLOT(m,n,p, PROP1, VALUE1, PROP2, VALUE2, ...) sets the
specified property-value pairs on the subplot axis. To add the
subplot to a specific figure pass the figure handle as the
value for the 'Parent' property.
If a SUBPLOT specification causes a new axis to overlap an
existing axis, the existing axis is deleted - unless the position
of the new and existing axis are identical. For example,
the statement SUBPLOT(1,2,1) deletes all existing axes overlapping
the left side of the Figure window and creates a new axis on that
side - unless there is an axes there with a position that exactly
matches the position of the new axes (and 'replace' was not specified),
in which case all other overlapping axes will be deleted and the
matching axes will become the current axes.
% snip
Note that subplots are numbered first from left to right, then by row - in other words, like a telephone dial. This is transposed from how just about everything else is numbered in MATLAB.
The orient Function
The orient function is used to change how the plot is oriented
on the page when printing. Note that it does not affect how the plot
looks on the screen. Furthermore, the orient command must
be used each time a new figure opens for that figure to have a specified
orientation.
What follows comes from MATLAB's help function in MATLAB R2009a[3] (some
paragraphs have been snipped out).
ORIENT Set paper orientation for printing.
ORIENT is used to set up the orientation of a Figure or Model
window for printing.
ORIENT LANDSCAPE causes subsequent PRINT operations from the current
Figure window to generate output in full-page landscape orientation
on the paper.
ORIENT ROTATED causes subsequent PRINT operations from the current
Figure window to generate output in full-page rotated orientation
on the paper.
ORIENT PORTRAIT causes subsequent PRINT operations from the current
Figure window to generate output in portrait orientation.
ORIENT TALL causes the current Figure window to map to the whole page
in portrait orientation for subsequent PRINT operations.
ORIENT, by itself, returns a string containing the paper
orientation, either PORTRAIT, LANDSCAPE, ROTATED or TALL
of the current Figure.
ORIENT(FIGHandle) or ORIENT(MODELName) returns the current
orientation of the Figure or Model.
ORIENT( FIG, ORIENTATION) specifies which figure to orient and how to
orient it based on the rules given above. ORIENTATION is one of
'landscape', 'portrait', 'rotated', or 'tall'.
% snip
The print Function
The print function is used to save a plot as a PostScript file.
What follows comes from MATLAB's help function in MATLAB R2009a[4] (some
paragraphs have been snipped out).
PRINT Print figure or model. Save to disk as image or M-file.
SYNTAX:
print
PRINT alone sends the current figure to your current printer.
The size and position of the printed output depends on the figure's
PaperPosition[mode] properties and your default print command
as specified in your PRINTOPT.M file.
% snip
print -device -options
You can optionally specify a print device (i.e., an output format such
as tiff or PostScript or a print driver that controls what is sent to
your printer) and options that control various characteristics of the
printed file (i.e., the resolution, the figure to print
etc.). Available devices and options are described below.
print -device -options filename
If you specify a filename, MATLAB directs output to a file instead of
a printer. PRINT adds the appropriate file extension if you do not
specify one.
% snip
SPECIFYING THE OUTPUT FILE:
<filename> % String on the command line
% snip
COMMON DEVICE DRIVERS
Output format is specified by the device driver input argument. This
argument always starts with '-d' and falls into one of several
categories:
% snip
Built-in MATLAB Drivers:
-dps % PostScript for black and white printers
-dpsc % PostScript for color printers
-dps2 % Level 2 PostScript for black and white printers
-dpsc2 % Level 2 PostScript for color printers
-deps % Encapsulated PostScript
-depsc % Encapsulated Color PostScript
-deps2 % Encapsulated Level 2 PostScript
-depsc2 % Encapsulated Level 2 Color PostScript
-dhpgl % HPGL compatible with Hewlett-Packard 7475A plotter
-dill % Adobe Illustrator 88 compatible illustration file
-djpeg<nn> % JPEG image, quality level of nn (figures only)
E.g., -djpeg90 gives a quality level of 90.
Quality level defaults to 75 if nn is omitted.
-dtiff % TIFF with packbits (lossless run-length encoding)
compression (figures only)
-dtiffnocompression % TIFF without compression (figures only)
-dpng % Portable Network Graphic 24-bit truecolor image
(figures only)
% snip
Example
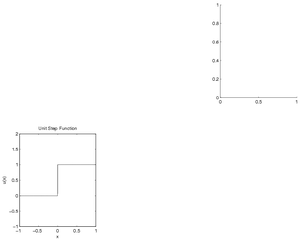
The following MATLAB code demonstrates how to fill the fourth window
of a 2x3 plot figure, save the figure as a PostScript file, and
preview it with kghostview; the resulting figure is in the thumbnail at right.
% Create a vector of numbers between -1 and 1 with 0.001 between numbers
x=-1:0.001:1;
%This formula for usf is one of several ways to define the unit step function
usf = @(t) t>=0;
%Create a figure with two rows of three figures and make subplot 4 (bottom row left) current
subplot(2,3,4)
% Plot the values of the function usf(x) against the vector x
plot(x, usf(x))
% Change the axes so the function is not covered by the subplot box
axis([-1, 1, -1, 2])
% Give the current subplot a title
title('Unit Step Function')
% Set the x-label
xlabel('x')
% Set the y-label
ylabel('u(x)')
% Make subplot 3 (top row right) current - it will be empty in the example
subplot(2,3,3)
% Use landscape (wide) orientation
orient landscape
% Send the current figure to a file named usfplot.eps;
% Note that the `.eps' is automatically added
print -deps usfplot
% The "!" character lets MATLAB act as if you were at a regular terminal.
% This command thus lets you view usfplot.eps using UNIX's kghostview
!kghostview usfplot.eps
General Plotting Tips
You must make sure that your data sets are presented properly. Here are some guidelines:
- Include axis labels that have, when appropriate, units. You should also include a description of the variable, or the variable itself, or both. For example, on p. 285 of Chapra[5], there is a plot of force versus velocity. Appropriate x axis labels would include any of the following:
xlabel('{\it v}, m/s')
xlabel('{\it v} (m/s)')
xlabel('Velocity, m/s')
xlabel('Velocity (m/s)')
xlabel('Velocity ({\it v}), m/s');
xlabel('Velocity ({\it v}, m/s)');
|
- You should be consistent within a single graph as far as which version you use, and you should pick which format you believe conveys the information most efficiently and effectively.
- Make sure your titles make sense and that you have your NET ID in one of the titles for each figure you create. If you have multiple subplots, you only need one of the titles to have your NET ID. Typically, the title will read "DEP. VAR vs. INDEP. VAR for DESCRIPTION (NET ID)" where DEP. VAR is your dependent variable (typically on the y axis), INDEP. VAR is your independent variable (typically on the x axis), DESCRIPTION is something that will differentiation this particular plot from others that might have the same variables (for example a data, or an experiment number), and NET ID is your NET ID.
- Data points should be represented by symbols and model equations should be represented by lines. Be sure to use a legend to identify each item plotted if there are multiple data sets on the same graph.
- Typically, you will want to set the axis limits such that no data point is on the figure boundary. Certainly you do not want a line to be plotted on top of a figure boundary. After you make a plot, if there is a data point on an edge, look at the current axes and go out a little bit. Just make sure if you end up fundamentally changing your code that you adjust the axes accordingly. Alternately, you can use the gzoom function below to automatically expand the graph.
- If you end up using the
hold oncommand, you should only use it after the first plotting command is issued; if not, there are some parts of a typical plot that will not show up, such as the complete plot frame.
Keeping Data Off The Edge
Typically, you will not want data points to land on the edge of a graph. If you are just plotting lines, this is not a problem but if you are actually putting symbols at each point, those symbols should not cross the border out of the axes. To combat this, you can put a short program called gzoom.m into your directory and run it. The default case is to add 10% to each direction of the graph in the active figure. The first argument specifies what the expansion value should be (if you want it different from 0.1) while the second argument specifies which figure should be expanded (if you want it to be different from the active figure). The gzoom function is:
function gzoom(n, f)
% gzoom.m
% Michael R. Gustafson II (mrg@duke.edu)
% Uploaded to pundit.pratt.duke.edu on September 6, 2008
%
% Function to determine the size of a figure window and increase the size
% GZOOM will increase figure 1 by a factor of
% 0.1 of the original size in each direction
% GZOOM(r) will increase figure 1 by a factor of
% r of the original size in each direction
% GZOOM(r, f) will increase figure f by a factor of
% r of the original size in each direction
if nargin==0
f=gca; n=0.1;
elseif nargin==1
f=gca;
end
v=axis;
xr = (v(2)-v(1));
yr = (v(4)-v(3));
axis(f, [v + n*[-xr xr -yr yr]]);
Here's how the code works:
- If there is no argument to the function, the variable f grabs a handle for the current axes - that is to say, it will be a reference to wherever you last plotted. Also, n will be 0.1 which means the figure will bump out by 10% of the original size in each direction.
- If there is only one argument, the variable f still grabs the current axes but the function will use the first argument as the bump out factor.
- The v=axis line will figure out the left, right, bottom, and top limits of the current figure; this will be a 1x4 matrix
- xr takes the difference between the right and left values - think of this as the x range
- yr takes the difference between the top and bottom values - think of this as the y range
- The final line sets the new limits of the axis by taking the old limits (v) and then bumping them by n times the appropriate range (x or y). The left and right are bumped to the left and right, respectively, by n*xr while the bottom and top are bumped down and up, respectively, by n*yr.
Using Different Line Styles
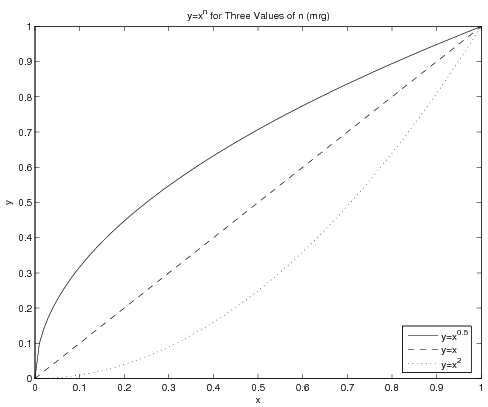
Most of the time, you will be plotting three or fewer different lines on a single window, and they can thus be distinguished from one another in MATLAB by using different line styles. There are two different ways to get multiple data sets plotted in the same figure - use the hold on...hold off paradigm or put all the "plot triplets" in a single plot command. What follows is an example of the latter case:
x = linspace(0, 1, 100);
y1 = x.^0.5;
y2 = x.^1;
y3 = x.^2;
plot(x, y1, 'k-', x, y2, 'k--', x, y3, 'k:');
legend('y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best');
title('y=x^n for Three Values of n (mrg)');
xlabel('x');
ylabel('y');
print -deps CurvePlot % note that adds .eps to filename
The figure this creates will be:
Note the legend - the use of the final arguments 'location', 'best' will make MATLAB look for the best spot in the window for the legend - which is to say, somewhere not conflicting with any of the lines if at all possible. Also note that the text in the legend and in the title contains basic LaTeX code for obtaining the superscripts.
Using Different Point Styles
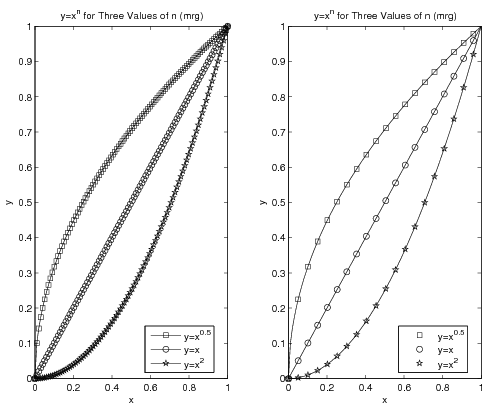
Sometimes there will be more data sets on a graph than there are line styles in MATLAB. In cases like this, you may think to use symbols at the points. The problem with that becomes clear if you have a large number of data points - you do not want to try to jam hundreds of symbols onto a curve. The left graph in the figure below shows what a disaster that could be. Instead, you can plot a line with all your data but plot points on top of the line with only some of the data. The right side of the figure shows the result of this operation. The code for both graphs in the figure is given below it.
x = linspace(0, 1, 100);
y1 = x.^0.5;
y2 = x.^1;
y3 = x.^2;
subplot(1,2,1) % left graph (ewwwwwww)
plot(x, y1, 'k-s', x, y2, 'k-o', x, y3, 'k-p');
legend('y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best');
title('y=x^n for Three Values of n (mrg)');
xlabel('x');
ylabel('y');
subplot(1,2,2) % right graph (ooo. aah. wow)
plot(x, y1, 'k-', x, y2, 'k-', x, y3, 'k-'); % lines only!
Incr = 5;
Indices = 1:Incr:length(x);
hold on % holds lines and now add points
PointPlot=plot(...
x(Indices), y1(Indices), 'ks',...
x(Indices), y2(Indices), 'ko',...
x(Indices), y3(Indices), 'kp');
hold off
legend(PointPlot, 'y=x^{0.5}', 'y=x', 'y=x^2', 'location', 'best');
title('y=x^n for Three Values of n (mrg)');
xlabel('x');
ylabel('y');
Note that the assignment of one of the plots to the variable PointPlot is required so that the legend can be told which set of
plots to use as a basis for the legend. Without this, it would be
possible for the legend to be based on the plot using solid lines (which are
the same for all three data sets) rather than to be based on the
plot using the symbols.
Using Different Scales
In the above example, two different scales were used for the data sets - a refined scale for the line and a rougher scale for the data points themselves. In other cases, it is the line that will need the rougher scale. As an example, assume you want MATLAB to numerically find the minimum of the function \(y=3x^2+11x-2\) using the built-in min command. To get the most precise answer possible, you will want to give MATLAB a very large number of points - say, 1 million. That code might look like:
P = [3 11 -2]
xVals = linspace(-3, 3, 1e6);
yVals = polyval(P, xVals);
yMin = min(yVals)
xMin = xVals(find(yVals==yMin))
Since the domain is 6 and there are 1e6 points, the spacing between points is approximately 6e-06. The x-coordinate of the answer then should be very close to the actual answer. In fact, MATLAB determines that the minimum value is -1.208333333332658e+01 and its x-coordinate is -1.833334833334833e+00 - very close to finding the minimum of y=-1.208333333333333e+01 at x=-1.833333333333333e+00
The problem, however, is that if you want to graph this, one million points is somewhat absurd. Unless you are planning to zoom in on the graph, there are around 1000x as many points as necessary/realistic/useful for a plot like this. Instead, you should either recalculate the equation using a smaller set of independent data or plot only some of the data. Code for the former might be:
xPlot = linspace(-3, 3, 100);
yPlot = polyval(P, xPlot);
plot(xPlot, yPlot, 'k-');
xlabel('x');
ylabel('y');
title('y=3x^2+11x-2 (mrg)');
grid on
print -deps PolyGraph
while code for the latter might be:
plot(xVals(1:1000:end), yVals(1:1000:end), 'k-');
xlabel('x');
ylabel('y');
title('y=3x^2+11x-2 (mrg)');
grid on
print -deps PolyGraph
The advantage of the first version above is that your domain definitely remains the same - the xPlot variable spans the same [-3, 3] as the xVals set even though it has three orders of magnitude fewer values. The disadvantage is that you will have to re-perform all the calculations on this new set.
The advantage of the second version, then, is that you are using prior data and thus do not have to recalculate anything. The disadvantage is, you might miss out on the tail end of the data. In the above example, going from 1 to 1e6 by 1e3 means the last value copied over will be 999001, meaning the maximum value used on the x-axis is xVals(999001) or approximately 2.994 instead of the 3 in the original. If that is a major concern, you should make sure the end of your refined data scale can be "reached" if your incremented indices start with 1 and have some increment. As an example, choosing to have 1000001 points in the original instead of 1000000 means going from 1 by 1e3 to 10000001 will actually end at the 10000001st, and last, point.
Putting Text on a Plot
The text(x, y, MyText)
command will plot the text string MyText at
the (x,y) coordinate. There are several important aspects to the text
command you must remember to use it properly.
First, the text command will not make the figure change its axes
to fit the data automatically. Clear the figure using clf then try typing:
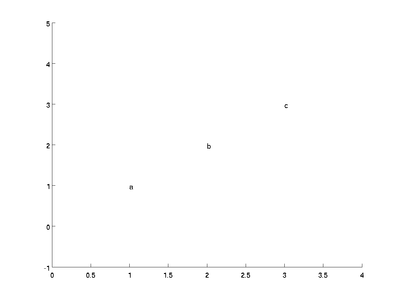
text([1; 2; 3], [1; 2; 3], ['a'; 'b'; 'c']);
and you will get the graph:
Note that the letter a is just visible at the top right corner
but b and care totally missing. You need to manually
changes the axes by using the axis command. In this case,
axis([0 4 -1 5])
will make the x axis go from 0 to 4 and the y axis go from -1 to 5, more than enough space to see all three letters:
Next, note that
text placed on plots stays until the next plotting command is
issued, so you can use multiple text commands to get several
labels on one plot. Also, the arguments can be column vectors which
allows multiple labels to be added at once (such as in the above
example). Note that row vectors do not work. Clear the figure
using clf then try the following:
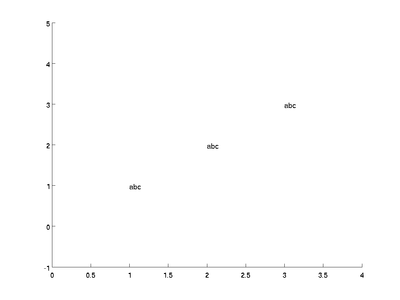
text([1 2 3], [1 2 3], ['a' 'b' 'c']);
axis([0 4 -1 5]);
This gives you:
Because you gave rows of labels instead of columns, text puts the
letters abc at each data point. In this case, you can solve the problem by transposing the third argument.
Also, the text must be...text. If you try to label using numbers you will get an error. Try
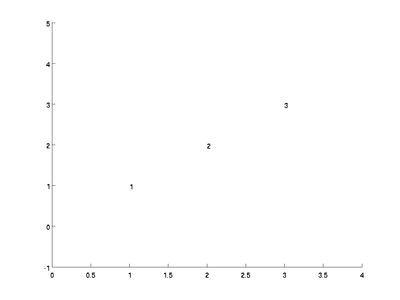
text([1; 2; 3], [1; 2; 3], [1; 2; 3]);
axis([0 4 -1 5]);
Fortunately, MATLAB has a command called num2str that will
convert numbers to strings. Clear the figure and try
text([1; 2; 3], [1; 2; 3], num2str([1; 2; 3]));
axis([0 4 -1 5]);
and you will get
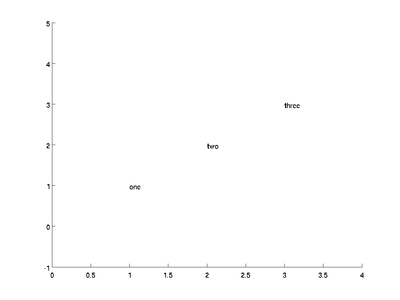
Finally, if you put multiple pieces of text on at once, they must all be
the same size. You can ensure that they are by using the char command. Clear the figure and try:
text([1; 2; 3], [1; 2; 3], char('one', 'two', 'three'))
axis([0 4 -1 5]);
The char command will automatically pad the shorter words with spaces, and the text command will give you:
Setting Limits and Tick Locations
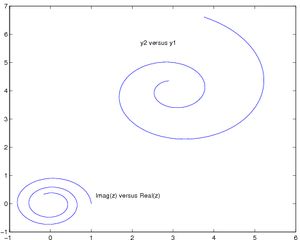
You can set the specific limits and tick locations for a graph such that they will not change when you resize the figure window and so that they print exactly as you see on the screen. To do this, you will use the set command with some specific arguments. The following example is modified from Palm, Chapter 5.2, on page 231 to create the specific figure as shown in the book:
% Code based on code from:
% Palm, Introduction to MATLAB for Engineers
% Chapter 5.2, p. 231
%% Initialize workspace and figure
clear, figure(1), clf
%% Original code (mostly)
x = -1:0.01:1;
y1 = 3+exp(-x).*sin(6*x);
y2 = 4+exp(-x).*cos(6*x);
plot((0.1+0.9i).^(0:0.01:10))
hold on
plot(y1, y2)
hold off
%% Add text and adjust limits and ticks
% Add text at specific locations, versus gtext
text(2.2, 5.7, 'y2 versus y1')
text(1.1, 0.3, 'Imag(z) versus Real(z)')
% Get current axis (gca) and change limits and ticks
set(gca, 'XLim', [-1 6], 'YLim', [-1 7],...
'XTick', -1:1:6, 'YTick', -1:1:7)
%% Print figure
print -deps PalmFig050204plot
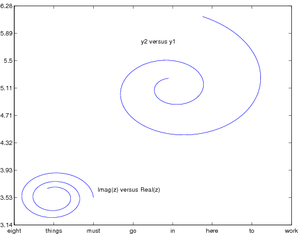
You can also specify what goes at each tick mark - either by giving a vector of values or a cell array of strings. Changing the set command as given below produces the graph at right:
set(gca, 'XLim', [-1 6], 'YLim', [-1 7],...
'XTick', -1:1:6, 'YTick', -1:1:7,...
'XTickLabel',...
{'eight', 'things', 'must', 'go', 'in', 'here', 'to', 'work'}, ...
'YTickLabel', ...
roundn(linspace(pi, 2*pi, 9), -2))
where the round(x,n) command rounds \(x\) to the nearest \(10^n\).
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.