Difference between revisions of "MATLAB:Fminbnd and fminsearch"
| Line 185: | Line 185: | ||
</source> | </source> | ||
| + | == Where the Mins Are == | ||
| + | As noted above, if you give MATLAB a domain with multiple local minima, it will not always find the most-minimum minima; here are two graphs showing 19,900 runs of <code>fminbnd</code> with different boundaries. The x axis represents the left boundary and the y axis represents the right boundary. | ||
| + | <center> | ||
| + | [[File:BasinLocations.png|300px]] | ||
| + | [[File:BasinValues.png|300px]] | ||
| + | </center> | ||
| + | The black regoins indicate left and right values that will not work since "Right" would be to the left of "Left" there. | ||
| + | There are four local minima over the entire domain from -10 to 10. In the left graph, with the locations, these are represented by | ||
| + | * Dark blue: (-9.5250, 2.0356) | ||
| + | * Cyan: (-3.2418, 2.6639) | ||
| + | * Yellow: (3.0414, 3.2922) | ||
| + | * Red: (9.4246, 3.9205) | ||
| + | In the right graph, with the values of the minimum, these are represented by: | ||
| + | * Dark blue: (-9.5250, 2.0356) | ||
| + | * Medium blue: (-3.2418, 2.6639) | ||
| + | * Cyan: (3.0414, 3.2922) | ||
| + | * Green: (9.4246, 3.9205) | ||
| + | For large enough domains, MATALAB will find one of the local minima; if the domain does not span a minimum, it will report back the minimum value at either the left or right boundary. If the domain spans multiple minima, it will report back one of the minima, though not always the minimum one. Notice when the domain is [-10 -4] the dark blue minimum is found, but when the domain is [-10 0], the cyan/medium blue minimum at -3.2418 is found -- even though its value (2.6639) is greater than the value at -9.5250. These graphs show that you need to make sure your domain is large enough to include the minimum you are trying to find but not so large as to include multiple minima. | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | The code for making these graphs is given in the expandable box here; click the "Expand" link at right. | ||
| + | <div class="mw-collapsible-content"> | ||
| + | <source lang="matlab"> | ||
| + | clear; format short e | ||
| + | |||
| + | MyFun = @(xa, ya, za) xa/10 + cos(xa) + sin(ya) + za | ||
| + | N = 200; | ||
| + | [xl, xr] = meshgrid(linspace(-10, 10, N)); | ||
| + | MyMinLoc = zeros(size(xl))-20; | ||
| + | MyMinVal = MyMinLoc; | ||
| + | |||
| + | for k=1:(N-1) | ||
| + | for l=(k+1):N | ||
| + | [MyMinLoc(l, k), MyMinVal(l, k)] = ... | ||
| + | fminbnd(@(xD) MyFun(xD, 1, pi), xl(l, k), xr(l, k)); | ||
| + | end | ||
| + | end | ||
| + | |||
| + | MyMap = jet; | ||
| + | |||
| + | figure(1); clf | ||
| + | %surfc(xl, xr, MyMinLoc) | ||
| + | imagesc(xl(1,:), xr(:,1), MyMinLoc, [-10 10]) | ||
| + | set(gca, 'YDir', 'Normal'), xlabel('Left'), ylabel('Right') | ||
| + | title('Locations of Minimum Found by fminbnd') | ||
| + | view(2), shading interp | ||
| + | colormap([0 0 0; MyMap]); BarH = colorbar; | ||
| + | set(BarH, 'YLim', [-10 max(MyMinLoc(:))]) | ||
| + | print -dpng -r0 BasinLocations | ||
| + | |||
| + | figure(2); clf | ||
| + | %surfc(xl, xr, MyMinLoc) | ||
| + | imagesc(xl(1,:), xr(:,1), MyMinVal, [2, 5.7]) | ||
| + | set(gca, 'YDir', 'Normal'), xlabel('Left'), ylabel('Right') | ||
| + | title('Values of Minimum Found by fminbnd') | ||
| + | view(2), shading interp | ||
| + | colormap([0 0 0; MyMap]); BarH = colorbar; | ||
| + | set(BarH, 'YLim', [2 5.6]) | ||
| + | print -dpng -r0 BasinValues | ||
| + | </source> | ||
| + | </div> | ||
| + | </div> | ||
<!-- | <!-- | ||
Revision as of 20:06, 28 September 2013
The fminbnd command in MATLAB can be used to find the value of a single parameter of a multivariable function that will minimize the value of the function on some bounded domain. The command can only find one minimum at a time and can only find minima based on one variable at a time. If there is a single local minimum over the domain, fminbnd should find it. If there are several, it should find one of them, though it may not find the most minimum minima. If there is no local minimum in the range, fminbnd will return one of the boundary values, depending on where the function is at its minimum value for the domain.
There are several different ways to present fminbnd with the specific function and variable.
Contents
Examples
Different Function Calls
Most General Case
The following examples show a method that will work regardless of how many input variables your function has or how you define your function - whether it is built-in, a variable containing an anonymous function, an anonymous function generated on the fly, or a .m file function. The paradigm is:
[INDEP_AT_MIN, FUNCTION_MIN] = fminbnd(@(DUMMY_VAR) FUNCTION_THING, LEFT_INDEP, RIGHT_INDEP)
where
- INDEP_AT_MIN is the calculated value of the requested variable when the function is at a minimum in the domain
- FUNCTION_MIN is the minimum value of the function at the INDEP_AT_MIN location
- DUMMY_VAR is the variable you want to use in this FUNCTION_THING to indicate which of the various inputs
fminbndis allowed to alter - FUNCTION_THING can be a built-in function, the name of an anonymous function, the name of a .m file function, or a calculation - whatever it is that you are trying to minimize; note that DUMMY_VAR must appear somewhere in this expression for
fminbndto be able to do anything - LEFT_INDEP, RIGHT_INDEP represent the minimum and maximum value of the range over which you want to minimize the function.
The example is based on wanting to determine minimum (and later, maximum) values of:
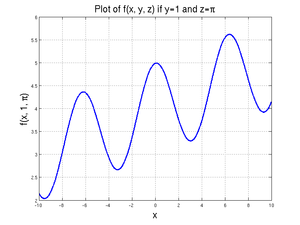
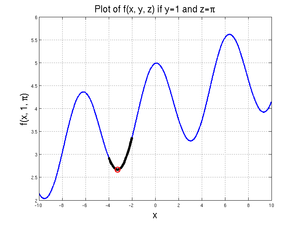
We will assume that two of the three variables (\(y\) and \(z\)) are known and that we want to find \(x\) given those values. We will further assume that \(y=1\) and \(z=\pi\). A graph of this function for values of \(x\) between -10 and 10 is shown at right.
Function on the Fly
If you only want to solve this problem once, and the calculation only requires one line of code, the process with the least "overhead" involves creating the function on the fly inside the fzero command. All you have to do is put your expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. You will also need to specify the boundary values.
The line:
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, 0, 5)
will produce
xValue =
3.0414e+00
fValue =
3.2922e+00
which has found the local minimum between \(x=0\) and \(x=5\).
Running the code:
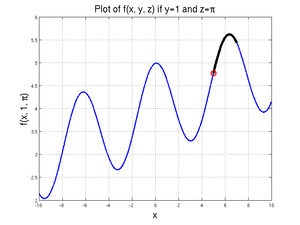
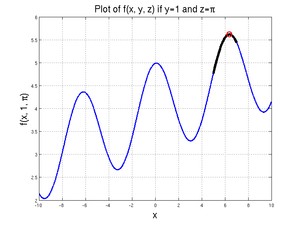
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, 5, 7)
will produce
xValue =
5.0000e+00
fValue =
4.7668e+00
since, for \(x\) values between 5 and 7, there is no local minimum. The value of the function at 5 is less than the value of the function at 7, so the 5 is returned.
Finally, for
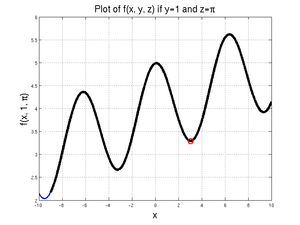
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, -9, 10)
MATLAB returns:
xValue =
3.0414e+00
fValue =
3.2922e+00
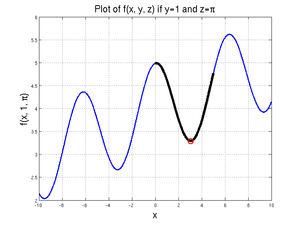
Note that this is not actually the "minimum" minimum - that would be at \(x=-3.2418\), where the function is 2.6639, as given by
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(1) + pi, -4, -2)
Furthermore, the actual minimum value of the function over the domain from -9 to 10 is given at \(x=-9\), where \(f=2.1719\); since MATLAB was able to find at least one local minimum, however, it did not check the boundary values.
A slightly "longer" version of this would have you pre-define the \(y\) and \(z\) variables first, then use the variables in the function definition: expression in for the FUNCTION_THING, making sure the DUMMY_VAR is appropriately used. The line:
y = 1;
z = pi;
[xValue, fValue] = fminbnd(@(xDummy) xDummy/10 + cos(xDummy) + sin(y) + z, -4, -2)
This works the same as the last example above - recall that when anonymous functions are created, they can take "snapshots" of the workspace. In the case above, the FUNCTION_THING is able to "see" what the variables y and z contain.
Pre-Defined Functions
If you want to solve the same problem multiple times, perhaps by altering initial guesses or altering one or more of the constant parameters in the function, you should first define the function. If the expression can be calculated all on one line, you may choose to use a variable with an anonymous function - for example:
MyFun = @(xa, ya, za) xa/10 + cos(xa) + sin(ya) + za
On the other hand, if the expression is more complicated or if you just want to put it in a .m file, you can certainly do that as well. or example, instead of the MyFun variable above, you could write a MyFun.m file containing:
function out = MyFun(xb, yb, zb)
out = xb/10 + cos(xb) + sin(yb) + zb;
In either case, you would use fminbnd by properly building the FUNCTION_THING using the name of the function. As in the previous example, you can hard-code the values for the \(x\) and \(y\) values:
[xValue, fValue] = fminbnd(@(xDummy) MyFun(xDummy, 1, pi), -4, 2)
or you can use variables to transmit the information:
y = 1;
z = pi;
[xValue, fValue] = fminbnd(@(xDummy) MyFun(xDummy, y, z), -4, 2)
In any event, note again that the FUNCTION_THING only has one unknown, and that unknown is named as the DUMMY_VAR.
==== Single-Variable Anonymous Functions ====
For single-variable anonymous functions, there is a slightly simpler way to run fminbnd - all you need to do is give the name of the variable to FUNCTION_THING rather than setting up the DUMMY_VAR. For example, to find the minimum value of \(x^2-\cos(x)=0\) on the domain from \(x\) going from -2 to 3, you can set up an anonymous function for it as:
MyAnonCalc = @(x) x.^2-cos(x)
and then solve with:
[xValue, fValue] = fminbnd(MyAnonCalc, -2, 3)
to get
xValue =
-4.5124e-07
fValue =
-1.0000e+00
Single-Variable Built-in Functions and .m Functions
The following method works for both built-in single-input functions and .m file single-input functions (i.e. not variables containing anonymous functions). The first argument is the name of the function in single quotes and the second argument is the initial guess or initial bracket for the one variable of the function. For example, to find the minimum value of \(\cos(x)\) for the domain of \(x\) going from 0 to 4, you can type
[xValue, fValue] = fminbnd('cos', 0, 4)
and get
xValue =
3.1416e+00
fValue =
-1.0000e+00
If you have a .m file function of one variable, the process is the same. For example, to find the minimum value of \(y=x^2-\cos(x)\) on a domain from -2 to 3, you could first create a .m file called MyCalc.m with:
function out = MyCalc(in)
out = in.^2 - cos(in);
then use fminbnd:
[xValue, fValue] = fminbnd('MyCalc', -2, 3)
and get
xValue =
-4.5124e-07
fValue =
-1.0000e+00
Finding Maximum Values
There is no fmaxbnd command. Conveniently, all you need to do to figure out the value and location of the maximum values would be to give fminbnd your function multiplied by -1. The only problem here is that the value of the function fminbnd returns will be the opposite of what you want. For example:
[xValue, fValueSignWrong] = fminbnd(@(xDummy) -(xDummy/10 + cos(xDummy) + sin(1) + pi), 5, 7)
will return
xValue =
6.3834e+00
fValueSignWrong =
-5.6164e+00
in order to get the actual value of the function at a maximum, you would need to re-run the calculation or just create a new variable that is equal to -1 multiplied by the function value MATLAB gave:
[xValue, fValueSignWrong] = fminbnd(@(xDummy) -(xDummy/10 + cos(xDummy) + sin(1) + pi), 5, 7)
fValue = -1*fValueSignWrong
to get
xValue =
6.3834e+00
fValueSignWrong =
-5.6164e+00
fValue =
5.6164e+00
Where the Mins Are
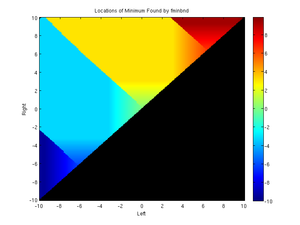
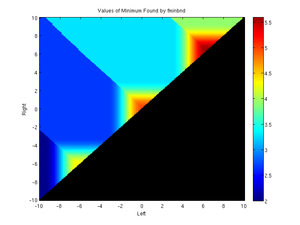
As noted above, if you give MATLAB a domain with multiple local minima, it will not always find the most-minimum minima; here are two graphs showing 19,900 runs of fminbnd with different boundaries. The x axis represents the left boundary and the y axis represents the right boundary.
The black regoins indicate left and right values that will not work since "Right" would be to the left of "Left" there. There are four local minima over the entire domain from -10 to 10. In the left graph, with the locations, these are represented by
- Dark blue: (-9.5250, 2.0356)
- Cyan: (-3.2418, 2.6639)
- Yellow: (3.0414, 3.2922)
- Red: (9.4246, 3.9205)
In the right graph, with the values of the minimum, these are represented by:
- Dark blue: (-9.5250, 2.0356)
- Medium blue: (-3.2418, 2.6639)
- Cyan: (3.0414, 3.2922)
- Green: (9.4246, 3.9205)
For large enough domains, MATALAB will find one of the local minima; if the domain does not span a minimum, it will report back the minimum value at either the left or right boundary. If the domain spans multiple minima, it will report back one of the minima, though not always the minimum one. Notice when the domain is [-10 -4] the dark blue minimum is found, but when the domain is [-10 0], the cyan/medium blue minimum at -3.2418 is found -- even though its value (2.6639) is greater than the value at -9.5250. These graphs show that you need to make sure your domain is large enough to include the minimum you are trying to find but not so large as to include multiple minima.
The code for making these graphs is given in the expandable box here; click the "Expand" link at right.
clear; format short e
MyFun = @(xa, ya, za) xa/10 + cos(xa) + sin(ya) + za
N = 200;
[xl, xr] = meshgrid(linspace(-10, 10, N));
MyMinLoc = zeros(size(xl))-20;
MyMinVal = MyMinLoc;
for k=1:(N-1)
for l=(k+1):N
[MyMinLoc(l, k), MyMinVal(l, k)] = ...
fminbnd(@(xD) MyFun(xD, 1, pi), xl(l, k), xr(l, k));
end
end
MyMap = jet;
figure(1); clf
%surfc(xl, xr, MyMinLoc)
imagesc(xl(1,:), xr(:,1), MyMinLoc, [-10 10])
set(gca, 'YDir', 'Normal'), xlabel('Left'), ylabel('Right')
title('Locations of Minimum Found by fminbnd')
view(2), shading interp
colormap([0 0 0; MyMap]); BarH = colorbar;
set(BarH, 'YLim', [-10 max(MyMinLoc(:))])
print -dpng -r0 BasinLocations
figure(2); clf
%surfc(xl, xr, MyMinLoc)
imagesc(xl(1,:), xr(:,1), MyMinVal, [2, 5.7])
set(gca, 'YDir', 'Normal'), xlabel('Left'), ylabel('Right')
title('Values of Minimum Found by fminbnd')
view(2), shading interp
colormap([0 0 0; MyMap]); BarH = colorbar;
set(BarH, 'YLim', [2 5.6])
print -dpng -r0 BasinValues
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.
External Links
References