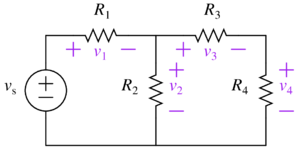Examples/Req
Contents
Simple Example
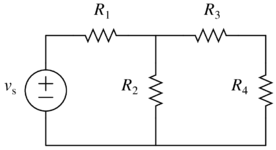
The following shows a step-by-step to find the equivalent resistance between two nodes for the following network:
Specifically, we will look at the equivalent resistance as seen by the voltage source and then use that information along with voltage division to get the individual voltages across the resistors.
Equivalent Resistance
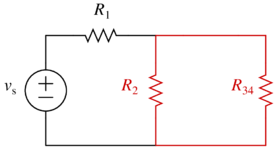
- First, look for any resistors in series or parallel from the perspective of the voltage sources nodes. At this point, $$R_3$$ and $$R_4$$ are in series so replace them with $$R_{34}=R_3+R_4$$:
 $$\longrightarrow$$
$$\longrightarrow$$
- Now, $$R_2$$ and $$R_{34}$$ are in parallel, so replace them with $$R_{234}=R_2||R_{34}$$:
 $$\longrightarrow$$
$$\longrightarrow$$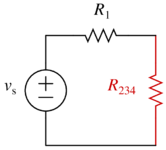
- These two resistors are in series, so $$R_{1234}=R_1+R_{234}$$.
- If you need to fully expand the equivalent resistances above, you can...
\( \begin{align*} R_{34}&=R_3+R_4\\ R_{234}&=R_2||R_{34}=\frac{R_2\cdot(R_3+R_4)}{R_2+R_3+R_4}=\frac{R_2R_3+R_2R_4}{R_2+R_3+R_4}\\ R_{1234}&=R_1+R_{234}=R_1+\frac{R_2R_3+R_2R_4}{R_2+R_3+R_4}= \frac{R_1R_2+R_1R_3+R_1R_4+R_2R_3+R_2R_4}{R_2+R_3+R_4} \end{align*} \)
- ...however, generally you will want to solve the problem symbolically with the equivalent resistor labels and then numerically solve for those.
Voltage Division
Now we can use voltage division to find the individual voltages across each resistor. We will use the following labels:
- The equivalent resistance $$R_{1234}$$ is the total resistance across which $$v_s$$ drops. Looking at the resistances in series in $$R_{1234}$$ tells us how we can divide the voltage. $$R_{1234}=R_1+R_{234}$$ which means it is comprised of two resistances in series - $$R_1$$ and $$R_{234}$$; that means we can find the voltage drop across either $$R_1$$ or $$R_{234}$$\[ \begin{align*} v_1&=v_s\frac{R_1}{R_{1234}} & v_{234}&=v_s\frac{R_{234}}{R_{1234}} \end{align*}\]
- The voltage drop across $$v_1$$ is one of the things we wanted to find. The voltage drop across $$R_{234}$$ happens to be between the same two nodes as $$R_2$$, so\[ \begin{align*} v_{2} &= v_{234}=v_s\frac{R_{234}}{R_{1234}} \end{align*}\]It is critically important to note here that the voltage division to get the voltage across $$R_2$$ uses the total resistance between the top-middle and bottom nodes. Voltage division is based upon dividing across series resistances, not necessarily individual resistors!
- At this point, we can see that the essential branch containing $$R_3$$ and $$R_4$$ is connected to the same nodes as $$R_2$$; that means to get the individual voltages across $$R_3$$ and $$R_4$$, we can redivide $$v_{234}$$ across those resistors\[ \begin{align*} v_3&=v_{234}\frac{R_3}{R_{34}} & v_4&=v_{234}\frac{R_4}{R_{34}}\\ v_3&=v_s\frac{R_{234}}{R_{1234}}\frac{R_3}{R_{34}}& v_4&=v_s\frac{R_{234}}{R_{1234}}\frac{R_4}{R_{34}}\\ \end{align*}\]Note that $$R_2$$ is not involved in the redivision.
- In summary\[ \begin{align*} R_{34}&=R_3+R_4 & R_{234}&=R_2||(R_3+R_4) & R_{1234}&=R_1+(R_2||(R_3+R_4)) \end{align*}\]\( \begin{align*} v_1 &=v_s\frac{R_1}{R_{1234}} & v_2 &=v_s\frac{R_{234}}{R_{1234}} & v_3 &=v_s\frac{R_{234}}{R_{1234}}\frac{R_3}{R_{34}} & v_4 &=v_s\frac{R_{234}}{R_{1234}}\frac{R_4}{R_{34}} \end{align*} \)
More Complicated Example
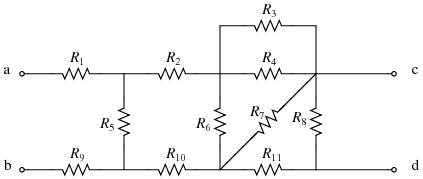
The following shows a step-by-step example to find the equivalent resistance between two nodes for the following network:
Each figure shows the "before" and "after" of a particular step. At the very end, the equivalent resistance for the network, but between two different notes, is shown.
\(R_{ab}\!\)
For the first example, we will find the equivalent resistance between nodes a and b.
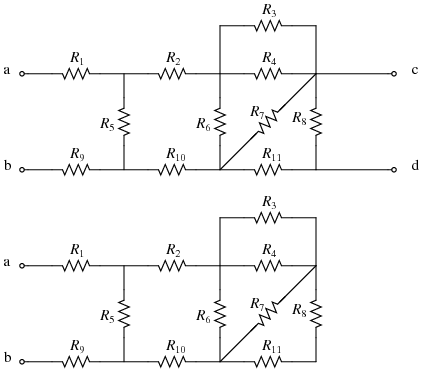
- Start by focusing only on nodes a and b
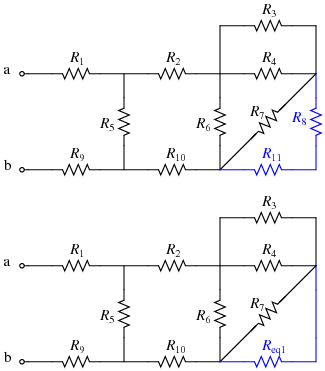
- Next, combine any resistances that are in series. In this particular case, R8 and R11 are now in series because the wire leading to node d has been eliminated. Replace this combination with Req1:
\(R_{eq1}=R_8+R_{11}\)
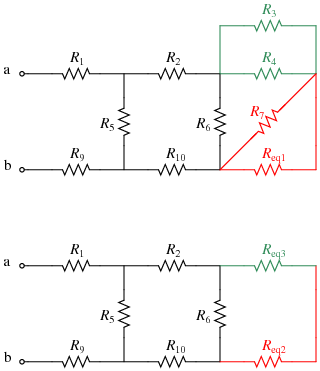
- Since no resistors are currently in series, now look for resistors that are in parallel. R7 and Req1 are in parallel; also, R3 and R4 are in parallel. Replace each with their equivalent resistances (named Req2 and Req3, respectively):
\(R_{eq2}=R_{eq1}||R_7=R_7||(R_8+R_{11})~~~~R_{eq3}=R_3||R_4~~~~\)
- Now note that Req2 and Req3 are in series; replace them with Req4:
\(R_{eq4}=R_{eq2}+R_{eq3}=(R_7||(R_8+R_{11}))+(R_3||R_4)\)
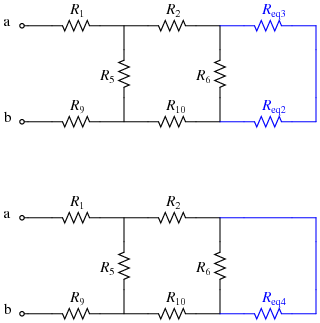
- After that step, R6 and Req4 are in parallel; replace them with Req5:
\(R_{eq5}=R_6||R_{eq4}=R_6||((R_7||(R_8+R_{11}))+(R_3||R_4))\)
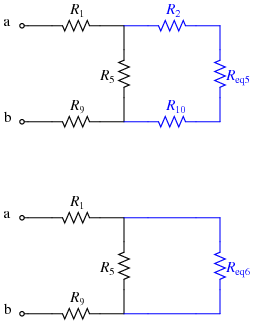
- Next, note that R2, Req5, and R10 are in series; replace them with Req6:
\(R_{eq6}=R_1+R_{eq5}+R_{10}=R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}\)
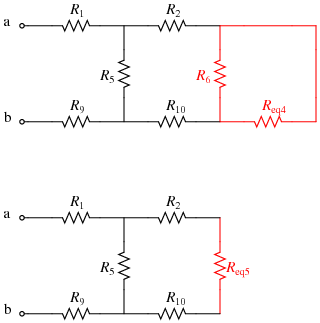
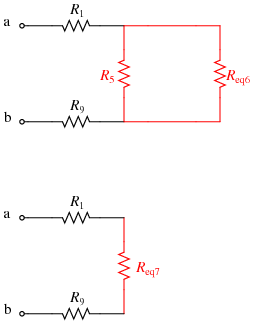
- Given that network, R5 and Req6 are in parallel; replace them with Req7:
\(R_{eq7}=R_5||R_{eq6}=R_5||(R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}) \)
- Finally, R1, Req7, and R9 are in series; replace them with Req,ab, the overall equivalent resistance between nodes a and b:
\(R_{eq,ab}=R_1+R_{eq7}+R_9=R_1+(R_5||(R_2+(R_6||((R_7||(R_8+R_{11}))+(R_3||R_4)))+R_{10}))+R_9\)
- Overall, this yields:
\( R_{eq,ab} = R_1~+~(R_5~||~(R_2~+~(R_6~||~((R_7~||~(R_8~+~R_{11}))+(R_3~||~R_4)))~+~R_{10}))~+~R_9\! \)
or, in other words,
punchline
\( \frac {R_{1}R_{2}R_{3}R_{4}R_{7}+R_{1}R_{2}R_{3}R_{4}R_{8}+R_{1}R_{2}R_{3}R_{4}R_{11}+R_{1}R_{2}R_{3}R_{6}R_{7}+R_{1}R_{2}R_{3}R_{6}R_{8}+R_{1}R_{2}R_{3}R_{6}R_{11}+R_{1}R_{2}R_{3}R_{7}R_{8}+R_{1}R_{2}R_{3}R_{7}R_{11}+R_{1}R_{2}R_{4}R_{6}R_{7}+R_{1}R_{2}R_{4}R_{6}R_{8}+R_{1}R_{2}R_{4}R_{6}R_{11}+R_{1}R_{2}R_{4}R_{7}R_{8}+R_{1}R_{2}R_{4}R_{7}R_{11}+R_{1}R_{3}R_{4}R_{5}R_{7}+R_{1}R_{3}R_{4}R_{5}R_{8}+R_{1}R_{3}R_{4}R_{5}R_{11}+R_{1}R_{3}R_{4}R_{6}R_{7}+R_{1}R_{3}R_{4}R_{6}R_{8}+R_{1}R_{3}R_{4}R_{6}R_{11}+R_{1}R_{3}R_{4}R_{7}R_{10}+R_{1}R_{3}R_{4}R_{8}R_{10}+R_{1}R_{3}R_{4}R_{10}R_{11}+R_{1}R_{3}R_{5}R_{6}R_{7}+R_{1}R_{3}R_{5}R_{6}R_{8}+R_{1}R_{3}R_{5}R_{6}R_{11}+R_{1}R_{3}R_{5}R_{7}R_{8}+R_{1}R_{3}R_{5}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{7}R_{8}+R_{1}R_{3}R_{6}R_{7}R_{10}+R_{1}R_{3}R_{6}R_{7}R_{11}+R_{1}R_{3}R_{6}R_{8}R_{10}+R_{1}R_{3}R_{6}R_{10}R_{11}+R_{1}R_{3}R_{7}R_{8}R_{10}+R_{1}R_{3}R_{7}R_{10}R_{11}+R_{1}R_{4}R_{5}R_{6}R_{7}+R_{1}R_{4}R_{5}R_{6}R_{8}+R_{1}R_{4}R_{5}R_{6}R_{11}+R_{1}R_{4}R_{5}R_{7}R_{8}+R_{1}R_{4}R_{5}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{7}R_{8}+R_{1}R_{4}R_{6}R_{7}R_{10}+R_{1}R_{4}R_{6}R_{7}R_{11}+R_{1}R_{4}R_{6}R_{8}R_{10}+R_{1}R_{4}R_{6}R_{10}R_{11}+R_{1}R_{4}R_{7}R_{8}R_{10}+R_{1}R_{4}R_{7}R_{10}R_{11}+R_{2}R_{3}R_{4}R_{5}R_{7}+R_{2}R_{3}R_{4}R_{5}R_{8}+R_{2}R_{3}R_{4}R_{5}R_{11}+R_{2}R_{3}R_{4}R_{7}R_{9}+R_{2}R_{3}R_{4}R_{8}R_{9}+R_{2}R_{3}R_{4}R_{9}R_{11}+R_{2}R_{3}R_{5}R_{6}R_{7}+R_{2}R_{3}R_{5}R_{6}R_{8}+R_{2}R_{3}R_{5}R_{6}R_{11}+R_{2}R_{3}R_{5}R_{7}R_{8}+R_{2}R_{3}R_{5}R_{7}R_{11}+R_{2}R_{3}R_{6}R_{7}R_{9}+R_{2}R_{3}R_{6}R_{8}R_{9}+R_{2}R_{3}R_{6}R_{9}R_{11}+R_{2}R_{3}R_{7}R_{8}R_{9}+R_{2}R_{3}R_{7}R_{9}R_{11}+R_{2}R_{4}R_{5}R_{6}R_{7}+R_{2}R_{4}R_{5}R_{6}R_{8}+R_{2}R_{4}R_{5}R_{6}R_{11}+R_{2}R_{4}R_{5}R_{7}R_{8}+R_{2}R_{4}R_{5}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}R_{9}+R_{2}R_{4}R_{6}R_{8}R_{9}+R_{2}R_{4}R_{6}R_{9}R_{11}+R_{2}R_{4}R_{7}R_{8}R_{9}+R_{2}R_{4}R_{7}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{6}R_{7}+R_{3}R_{4}R_{5}R_{6}R_{8}+R_{3}R_{4}R_{5}R_{6}R_{11}+R_{3}R_{4}R_{5}R_{7}R_{9}+R_{3}R_{4}R_{5}R_{7}R_{10}+R_{3}R_{4}R_{5}R_{8}R_{9}+R_{3}R_{4}R_{5}R_{8}R_{10}+R_{3}R_{4}R_{5}R_{9}R_{11}+R_{3}R_{4}R_{5}R_{10}R_{11}+R_{3}R_{4}R_{6}R_{7}R_{9}+R_{3}R_{4}R_{6}R_{8}R_{9}+R_{3}R_{4}R_{6}R_{9}R_{11}+R_{3}R_{4}R_{7}R_{9}R_{10}+R_{3}R_{4}R_{8}R_{9}R_{10}+R_{3}R_{4}R_{9}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}R_{8}+R_{3}R_{5}R_{6}R_{7}R_{9}+R_{3}R_{5}R_{6}R_{7}R_{10}+R_{3}R_{5}R_{6}R_{7}R_{11}+R_{3}R_{5}R_{6}R_{8}R_{9}+R_{3}R_{5}R_{6}R_{8}R_{10}+R_{3}R_{5}R_{6}R_{9}R_{11}+R_{3}R_{5}R_{6}R_{10}R_{11}+R_{3}R_{5}R_{7}R_{8}R_{9}+R_{3}R_{5}R_{7}R_{8}R_{10}+R_{3}R_{5}R_{7}R_{9}R_{11}+R_{3}R_{5}R_{7}R_{10}R_{11}+R_{3}R_{6}R_{7}R_{8}R_{9}+R_{3}R_{6}R_{7}R_{9}R_{10}+R_{3}R_{6}R_{7}R_{9}R_{11}+R_{3}R_{6}R_{8}R_{9}R_{10}+R_{3}R_{6}R_{9}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{9}R_{10}+R_{3}R_{7}R_{9}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}R_{8}+R_{4}R_{5}R_{6}R_{7}R_{9}+R_{4}R_{5}R_{6}R_{7}R_{10}+R_{4}R_{5}R_{6}R_{7}R_{11}+R_{4}R_{5}R_{6}R_{8}R_{9}+R_{4}R_{5}R_{6}R_{8}R_{10}+R_{4}R_{5}R_{6}R_{9}R_{11}+R_{4}R_{5}R_{6}R_{10}R_{11}+R_{4}R_{5}R_{7}R_{8}R_{9}+R_{4}R_{5}R_{7}R_{8}R_{10}+R_{4}R_{5}R_{7}R_{9}R_{11}+R_{4}R_{5}R_{7}R_{10}R_{11}+R_{4}R_{6}R_{7}R_{8}R_{9}+R_{4}R_{6}R_{7}R_{9}R_{10}+R_{4}R_{6}R_{7}R_{9}R_{11}+R_{4}R_{6}R_{8}R_{9}R_{10}+R_{4}R_{6}R_{9}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{9}R_{10}+R_{4}R_{7}R_{9}R_{10}R_{11}}{R_{2}R_{3}R_{4}R_{7}+R_{2}R_{3}R_{4}R_{8}+R_{2}R_{3}R_{4}R_{11}+R_{2}R_{3}R_{6}R_{7}+R_{2}R_{3}R_{6}R_{8}+R_{2}R_{3}R_{6}R_{11}+R_{2}R_{3}R_{7}R_{8}+R_{2}R_{3}R_{7}R_{11}+R_{2}R_{4}R_{6}R_{7}+R_{2}R_{4}R_{6}R_{8}+R_{2}R_{4}R_{6}R_{11}+R_{2}R_{4}R_{7}R_{8}+R_{2}R_{4}R_{7}R_{11}+R_{3}R_{4}R_{5}R_{7}+R_{3}R_{4}R_{5}R_{8}+R_{3}R_{4}R_{5}R_{11}+R_{3}R_{4}R_{6}R_{7}+R_{3}R_{4}R_{6}R_{8}+R_{3}R_{4}R_{6}R_{11}+R_{3}R_{4}R_{7}R_{10}+R_{3}R_{4}R_{8}R_{10}+R_{3}R_{4}R_{10}R_{11}+R_{3}R_{5}R_{6}R_{7}+R_{3}R_{5}R_{6}R_{8}+R_{3}R_{5}R_{6}R_{11}+R_{3}R_{5}R_{7}R_{8}+R_{3}R_{5}R_{7}R_{11}+R_{3}R_{6}R_{7}R_{8}+R_{3}R_{6}R_{7}R_{10}+R_{3}R_{6}R_{7}R_{11}+R_{3}R_{6}R_{8}R_{10}+R_{3}R_{6}R_{10}R_{11}+R_{3}R_{7}R_{8}R_{10}+R_{3}R_{7}R_{10}R_{11}+R_{4}R_{5}R_{6}R_{7}+R_{4}R_{5}R_{6}R_{8}+R_{4}R_{5}R_{6}R_{11}+R_{4}R_{5}R_{7}R_{8}+R_{4}R_{5}R_{7}R_{11}+R_{4}R_{6}R_{7}R_{8}+R_{4}R_{6}R_{7}R_{10}+R_{4}R_{6}R_{7}R_{11}+R_{4}R_{6}R_{8}R_{10}+R_{4}R_{6}R_{10}R_{11}+R_{4}R_{7}R_{8}R_{10}+R_{4}R_{7}R_{10}R_{11}} \)
\(R_{cd}\!\)
The resistance between nodes \(c\) and \(d\) will be different because of how the resistors appear to the paths between those two nodes. Specifically, the equivalent resistance between those two terminals is:
\( R_{eq,cd} = (((((R_2~+~R_5~+~R_{10})~||~R_6)~+~(R_3~||~R_4))~||~R_7)~+~R_{11})~||~R_8 \)
Note that resistors \(R_1\) and \(R_9\) are not involved in this equivalent.